题目内容
【题目】某市三景区是人们节假日游玩的热点景区,某学校对九(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别,A:三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩,现根据调查结果绘制了不完全的条形统计图和扇形统计图如下:
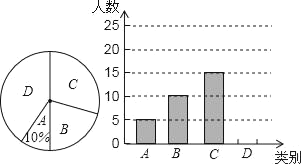
请结合图中信息解答下列问题:
(1)九(1)班现有学生 人,在扇形统计图中表示“B类别”的扇形的圆心角的度数为 ;
(2)请将条形统计图补充完整;
(3)若该校九年级有1000名学生,求计划“五一”小长假随父母到这三个景区游玩的学生多少名?
【答案】(1)50,72°;(2)补图见解析;(3)600名
【解析】
(1)由A类5人,占10%,可求得总人数,继而求得B类别占的百分数,则可求得“B类别”的扇形的圆心角的度数;
(2)首先求得D类别的人数,则可将条形统计图补充完整;
(3)利用总人数乘以对应的比例即可求解.
解:(1)∵A类5人,占10%,
∴八(1)班共有学生有:5÷10%=50(人);
∴在扇形统计图中,表示“B类别”的扇形的圆心角的度数为:![]() ×360°=72°;
×360°=72°;
故答案为50,72°;
(2)D类:50﹣5﹣10﹣15=20(人),如图:
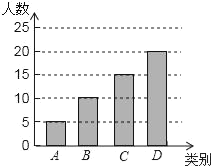 ;
;
(3)计划“五一”小长假随父母到这三个景区游玩的学生人数是1000×(1﹣![]() )=600(人).
)=600(人).
答:计划“五一”小长假随父母到这三个景区游玩的学生人数是600人.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案【题目】某水果公司新购进10000千克柑橘,每千克柑橘的成本为9元. 柑橘在运输、存储过程中会有损坏,销售人员从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录如下:
柑橘总重量n/千克 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
损坏柑橘重量m/千克 | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.54 |
柑橘损坏的频率 | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
根据以上数据,估计柑橘损坏的概率为 (结果保留小数点后一位);由此可知,去掉损坏的柑橘后,水果公司为了不亏本,完好柑橘每千克的售价至少为________元.
【题目】为了解早高峰期间A,B两邻近地铁站乘客的乘车等待时间(指乘客从进站到乘上车的时间),某部门在同一上班高峰时段对A、B两地铁站各随机抽取了500名乘客,收集了其乘车等待时间(单位:分钟)的数据,统计如表:
等待时的频数间 乘车等待时间 地铁站 | 5≤t≤10 | 10<t≤15 | 15<t≤20 | 20<t≤25 | 25<t≤30 | 合计 |
A | 50 | 50 | 152 | 148 | 100 | 500 |
B | 45 | 215 | 167 | 43 | 30 | 500 |
据此估计,早高峰期间,在A地铁站“乘车等待时间不超过15分钟”的概率为_____;夏老师家正好位于A,B两地铁站之间,她希望每天上班的乘车等待时间不超过20分钟,则她应尽量选择从_____地铁站上车.(填“A”或“B”)