Question

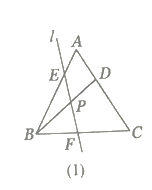
【题目】问题：如图1，△ABC中，AB＝a，∠ACB＝α．如何用直尺和圆规作出点P，均使得∠APB＝α？（不需解答）

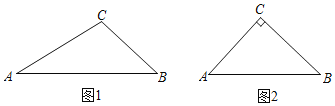
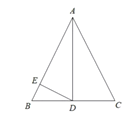
尝试：如图2，△ABC中，AC＝BC，∠ACB＝90°．

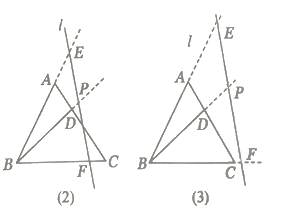
（1）请用直角三角尺（仅可画直角或直线）在图2中画出一个点P，使得∠APB＝45°

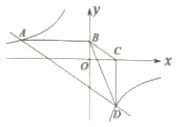
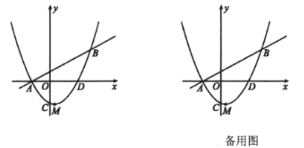
（2）如图3，若AC＝BC＝，以点A为原点，直线AB为x轴，过点A垂直于AB的直线为y轴建立平面直角坐标系，直线y＝（b≥0）交x轴于点M，交y轴与点N．

①当b＝7+时，请仅用圆规在射线MN上作出点P，使得∠APB＝45°；

②请直接写出射线MN上使得∠APB＝45°或∠APB＝135°时点P的个数及相应的b的取值范围；

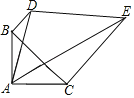
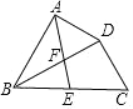
③应用：如图4，△ABC中，AB＝a，∠ACB＝α，请用直尺和圆规作出点P，使得∠APB＝α，且AP+BP最大，请简要说明理由．（不写作法，保留作图痕迹）

Answer 1

【答案】（1）见解析；（2）①见解析；②当0≤b≤2或b＝3+3时，满足条件的点P只有一个；当2＜b＜3+3时，满足条件的点P有两个；当b＞3+3时，满足条件的点P为0个；③见解析；

【解析】

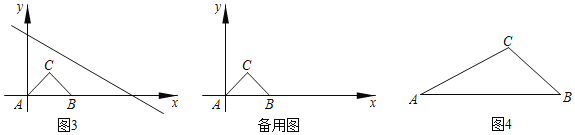
（1）以C为圆心CA为半径作⊙C，在优弧AB上任意取一点P，连接PA，PB，点P即为所求．

（2）①如图3中，过点C作CE∥MN，交OM于E，作EF⊥MN于F．以C为圆心，CA为半径作⊙C，通过计算说明⊙C与MN有两个交点P1，P2，P1，P2即为所求．

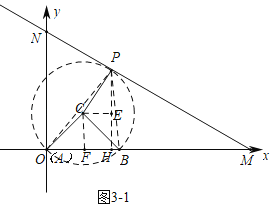
②如图3﹣1中，当⊙C与直线MN与⊙C相切于点P时，作PH⊥OM于H，CF⊥OM于F，CE⊥PH于E．求出相切时b的值以及直线MN经过点B时b的值即可判断．

应用：如图4中，作△ABC的外接圆，AB的垂直平分线交△ABC的外接圆于M．点M（即点P）即为所求．

解：（1）如图2中，点P即为所求．

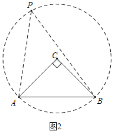
（2）①如图3中，过点C作CE∥MN，交OM于E，作EF⊥MN于F．

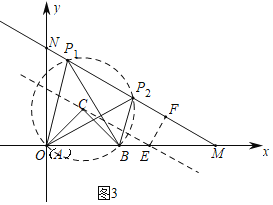
∵AC＝CB＝，∠ACB＝90°，

∴OB＝ OC＝2，可得C（，），

∵CE∥MN，直线MN的解析式为y＝﹣x+（7+），

∴直线CE的解析式为y＝﹣x++1，

∴E（3+，0），由题意M（7+，0），

∴EM＝4，

∵EF⊥MN，∠EMF＝30°，

∴EF＝2，

以C为圆心，CA为半径作⊙C，

∵2＜，

∴⊙C与MN有两个交点P1，P2，连接OP1，BP1，OP2，BP2，

∴∠AP1B＝∠ACB＝45°，∠AP2B＝∠ACB＝45°，

∴P1，P2即为所求．

②如图3﹣1中，当⊙C与直线MN与⊙C相切于点P时，作PH⊥OM于H，CF⊥OM于F，CE⊥PH于E．

在Rt△PCE中，∵∠PEC＝90°，∠CPE＝30°，PC＝，

∴CE＝PC＝，PE＝CE＝，

∵四边形CFHE是矩形，

∴FH＝CE＝，CF＝EH＝，

∴PH＝PE+EH＝+，

在Rt△PHM中，∵∠PHM＝90°，∠PMH＝30°，

∴MH＝PH＝3+，

∴OM＝OF+FH+HM＝++3+＝3+3，

∴b＝3+3，

当直线MN经过点B时，b＝2，

观察图象可知：当0≤b≤2或b＝3+3时，满足条件的点P只有一个．

当2＜b＜3+3时，满足条件的点P有两个．

当b＞3+3时，满足条件的点P为0个．

应用：如图4中，作△ABC的外接圆，AB的垂直平分线交△ABC的外接圆于M．

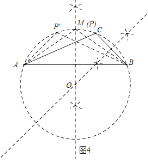
在劣弧AB上任意取一点P′，连接P′A，P′B，则∠AP′B＝∠ACB＝α，

当点P′与M重合时，PA+PB的值最大，

如图，点P即为所求．