题目内容
【题目】阅读下面材料:
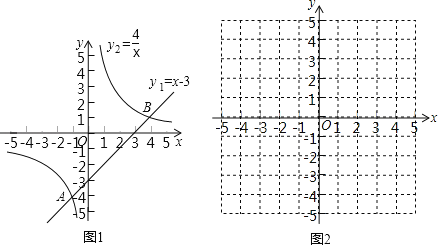
学习函数知识后,对于一些特殊的不等式,我们可以借助函数图象来求出它的解集,例如求不等式x﹣3>![]() 的解集,我们可以在同一坐标系中,画出直线y1=x﹣3与函数y2=
的解集,我们可以在同一坐标系中,画出直线y1=x﹣3与函数y2=![]() 的图象(如图1),观察图象可知:它们交于点A(﹣1,﹣4),B(4,1).当﹣1<x<0,或x>4时,y1>y2,即不等式x﹣3>
的图象(如图1),观察图象可知:它们交于点A(﹣1,﹣4),B(4,1).当﹣1<x<0,或x>4时,y1>y2,即不等式x﹣3>![]() 的解集为﹣1<x<0,或x>4.
的解集为﹣1<x<0,或x>4.
小东根据学习以上知识的经验,对求不等式x3+3x2﹣x﹣3>0的解集进行了探究.下面是小东的探究过程,请补充完整:
(1)将不等式按条件进行转化:当x=0时,原不等式不成立;x>0时,原不等式转化为x2+3x﹣1>![]() ;当x<0时,原不等式转化为______;
;当x<0时,原不等式转化为______;
(2)构造函数,画出图象:设y3=x2+3x﹣1,y4=![]() ,在同一坐标系(图2)中分别画出这两个函数的图象.
,在同一坐标系(图2)中分别画出这两个函数的图象.
(3)借助图象,写出解集:观察所画两个函数的图象,确定两个函数图象交点的横坐标,结合(1)的讨论结果,可知:不等式x3+3x2﹣x﹣3>0的解集为______.
【答案】(1)x2+3x﹣1<![]() ;(2)画图见解析;(3)﹣3<x<﹣1或x>1.
;(2)画图见解析;(3)﹣3<x<﹣1或x>1.
【解析】
(1)根据不等式的基本性质,不等式的两边同时除以一个负数,不等号的方向发生改变,先在不等式的两边同时除以x,在移项即可;
(2)根据列表,描点,连线的步骤画出y3=x2+3x﹣1与y4=![]() 的图象即可;
的图象即可;
(3)观察函数图象即可确定交点坐标,再根据(1)中的变形观察图象即可.
(1)由题意得:当x<0时,x2+3x﹣1-![]() <0,
<0,
∴x2+3x﹣1<![]()
故答案为:x2+3x﹣1<![]() ;
;
(2)列表:
x | -4 | -3 | -2 | -1.5 | -1 | 0 | 1 | ||||||
y3=x2+3x﹣1 | 3 | -1 | -3 | -3.25 | -3 | -1 | 3 | ||||||
x | -3 | -2 | -1 | 1 | 2 | 3 | |||||||
y4= | -1 | -1.5 | -3 | 3 | 1.5 | 1 | |||||||
描点、连线,画出y3=x2+3x﹣1与y4=![]() 的图象如图所示:
的图象如图所示:
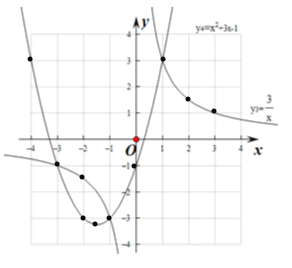
(3)由(1)可得:不等式x3+3x2﹣x﹣3>0当x>0时,可转化为x2+3x﹣1>![]() ;当x<0时,可转化为x2+3x﹣1<
;当x<0时,可转化为x2+3x﹣1<![]() ,
,
由图象可得:不等式x3+3x2﹣x﹣3>0的解集为:﹣3<x<﹣1或x>1;
故答案为:﹣3<x<﹣1或x>1.

【题目】大学生小张利用暑假50天在一超市勤工俭学,被安排销售一款成本为40元/件的新型商品,此类新型商品在第x天的销售量p件与销售的天数x的关系如下表:
x(天) | 1 | 2 | 3 | … | 50 |
p(件) | 118 | 116 | 114 | … | 20 |
销售单价q(元/件)与x满足:当1≤x<25时q=x+60;当25≤x≤50时q=40+![]() .
.
(1)请分析表格中销售量p与x的关系,求出销售量p与x的函数关系.
(2)求该超市销售该新商品第x天获得的利润y元关于x的函数关系式.
(3)这50天中,该超市第几天获得利润最大?最大利润为多少?