题目内容
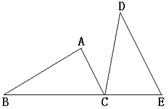
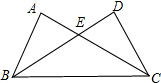
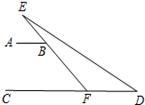
已知:如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
求证: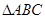 ≌
≌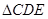 .
.
求证:
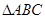 ≌
≌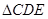 .
.
AAS.
试题分析:根据两直线AC∥DE,可以证得∠ACD=∠D(内错角相等),∠BCA=∠E(同位角相等),通过等量代换可知∠B=∠D,再根据线段AC=CE,可证两个△ABC≌△CDE,然后根据等边三角形的的性质BC=DE.
试题解析:∵AC∥DE,
∴∠ACD=∠D,∠BCA=∠E.
又∵∠ACD=∠B,
∴∠B=∠D.
在△ABC和△CDE中,
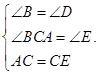
∴△ABC≌△CDE(AAS).
∴BC=DE.

练习册系列答案
相关题目
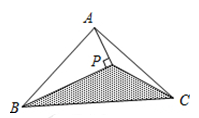
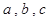 是三角形的三边,则
是三角形的三边,则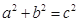
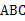 中,∠
中,∠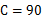 °,所以
°,所以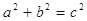
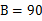 °,所以
°,所以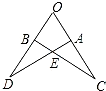
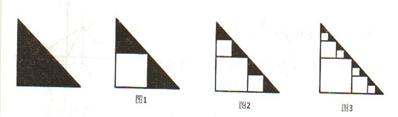
 ;再分别从剩下的两个三角形内用同样的方式裁剪下两个正方形,如图2所示,设所得到的剩余部分的面积为
;再分别从剩下的两个三角形内用同样的方式裁剪下两个正方形,如图2所示,设所得到的剩余部分的面积为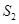 ;再分别从剩余的四个三角形内用同样的方式裁剪下四个正方形,如图3所示,设所得到的剩余部分的面积为
;再分别从剩余的四个三角形内用同样的方式裁剪下四个正方形,如图3所示,设所得到的剩余部分的面积为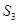 ;.........,如此下去,第n个裁剪后得到的剩余部分面积
;.........,如此下去,第n个裁剪后得到的剩余部分面积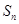 =
= 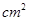 .
.