题目内容
【题目】如图,将一个三角板![]() ,绕点
,绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() ,得到
,得到![]() ,连接
,连接![]() ,且
,且![]() ,
,![]() ,则线段
,则线段![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
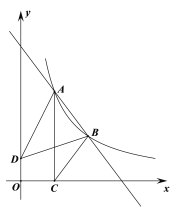
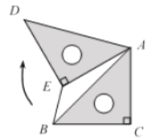
连接![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,根据旋转性质可知AB=AD,∠DAB=60°,∠AED=90°,AE=DE=AC=BC=2,由此得出△ABD为等边三角形,然后进一步通过证明△BAE△BDE得出∠ABE=∠DBE,根据等腰三角形“三线合一”可知BF⊥AD,且AF=DF,由此利用勾股定理分别计算出AB、BF的长,最后通过BE=BFEF进一步计算即可得出答案.
,根据旋转性质可知AB=AD,∠DAB=60°,∠AED=90°,AE=DE=AC=BC=2,由此得出△ABD为等边三角形,然后进一步通过证明△BAE△BDE得出∠ABE=∠DBE,根据等腰三角形“三线合一”可知BF⊥AD,且AF=DF,由此利用勾股定理分别计算出AB、BF的长,最后通过BE=BFEF进一步计算即可得出答案.

如图,连接![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,
,
由旋转可知,AB=AD,∠DAB=60°,∠AED=90°,AE=DE=AC=BC=2,
∴△ABD为等边三角形,
∴AB=BD,
在△BAE与△BDE中,
∵AE=DE,BA=BD,BE=BE,
∴△BAE△BDE(SSS),
∴∠ABE=∠DBE,
根据等腰三角形“三线合一”可得BF⊥AD,且AF=DF,
∵AC=BC=2,∠ACB=90°,
∴AB=![]() ,
,
∴AB=BD=AD=![]() ,
,
∴AF=![]() ,
,
∴BF=![]() ,
,
∵∠AED=90°,AE=DE,
∴∠FAE=45°,
∵BF⊥AD,
∴∠FEA=45°,
∴EF=AF=![]() ,
,
∴BE=BFEF=![]() ,
,
故选:A.

 阅读快车系列答案
阅读快车系列答案【题目】学校组织甲、乙两组同学参加国学经典知识对抗赛,每组有![]() 位选手,每场比赛两组各派
位选手,每场比赛两组各派![]() 人进行现场对抗比赛,满分为
人进行现场对抗比赛,满分为![]() 分,共进行了
分,共进行了![]() 场比赛.学校整理和汇总了这
场比赛.学校整理和汇总了这![]() 场比赛的成绩,并制成如下所示的尚不完整的统计表和图所示的折线统计图.
场比赛的成绩,并制成如下所示的尚不完整的统计表和图所示的折线统计图.
场次 | 一 | 二 | 三 | 四 | 五 | 六 |
甲组成绩 (单位:分) |
|
|
|
|
|
|
乙组成绩 (单位:分) |
|
|
|
|
|
|
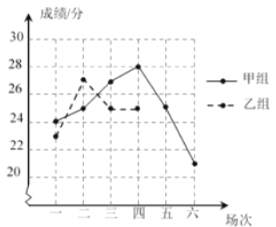
根据以上信息回答下面的问题:
(1)若甲、乙两组成绩的平均数相同,
①求![]() 的值;
的值;
②将折线统计图补充完整,并根据折线统计图判断哪组成绩比较稳定.
(2)若甲、乙两组成绩的中位数相等,直接写出![]() 的最小值.
的最小值.
(3)在(1)中的条件下,若从所有成绩为![]() 分的选手中随机抽取两人对其答题情况进行分析,请用列表法求抽到的两位选手均来自同一组的概率.
分的选手中随机抽取两人对其答题情况进行分析,请用列表法求抽到的两位选手均来自同一组的概率.