题目内容
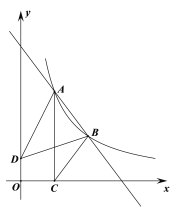
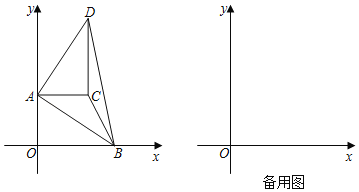
【题目】如图,在平面直角坐标系中,O为原点,点A(0,10),点B(m,0),且m>0,把△AOB绕点A逆时针旋转90°,得到△ACD,点O,B旋转后的对应点分别为点C,D.
(1)点C的坐标为 ;
(2)①设△BCD的面积为S,用含m的代数式表示S,并直接写出m的取值范围;
②当S=12时,请直接写出点B的坐标.
【答案】(1)(10,10);(2)①S=![]() m2﹣5m(m>10)或S=﹣
m2﹣5m(m>10)或S=﹣![]() m2+5m(0<m<10);②点B的坐标为(12,0)或(4,0)或(6,0).
m2+5m(0<m<10);②点B的坐标为(12,0)或(4,0)或(6,0).
【解析】
(1)根据旋转的性质得到AC=AO=10,∠OAC=90°,得到点C的坐标;
(2)①分点E在线段OB上、点E在线段OB的延长线上两种情况,根据三角形的面积公式计算;
②把S=12分别代入函数关系式,计算即可.
(1)∵点A(0,10),
∴AO=10,
∵△AOB绕点A逆时针旋转90°得△ACD,
∴AC=AO=10,∠OAC=90°,
∴C(10,10),
故答案为:(10,10);
(2)①延长DC交x轴于点E,
∵点B(m,0),
∴OB=m,
∵△AOB绕点A逆时针旋转90°得△ACD,
∴DC=OB=m,∠ACD=∠AOB=90°,∠OAC=90°,
∴∠ACE=90°,
∴四边形OACE是正方形,
∴DE⊥x轴,OE=AC=10,
如图1,当点E在线段OB上时,
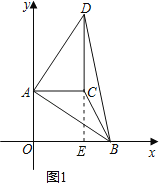
BE=OB﹣OE=m﹣10,
∴S=![]() DCBE=
DCBE=![]() m(m﹣10),
m(m﹣10),
即S=![]() m2﹣5m(m>10),
m2﹣5m(m>10),
如图2,当点E在线段OB的延长线上(点B不与O,E重合)时,

则BE=OE﹣OB=10﹣m,
∴S=![]() DCBE=
DCBE=![]() m(10﹣m),
m(10﹣m),
即S=﹣![]() m2+5m(0<m<10),
m2+5m(0<m<10),
当点B与E重合时,即m=10,△BCD不存在,
综上所述,S=![]() m2﹣5m(m>10)或S=﹣
m2﹣5m(m>10)或S=﹣![]() span>m2+5m(0<m<10);
span>m2+5m(0<m<10);
②当S=12,m>10时,![]() m2﹣5m=12,
m2﹣5m=12,
解得:m1=﹣2(舍去),m2=12,
当S=12,0<m<10时,﹣![]() m2+5m=12,
m2+5m=12,
解得:m3=4,m4=6,
∴点B的坐标为(12,0)或(4,0)或(6,0).