Question

【题目】如图，△ABC是边长为4个等边三角形，D为AB边的中点，以CD为直径画圆，则图中阴影部分的面积为（结果保留π）．

Answer 1

【答案】2.5 ﹣π
【解析】解：过点O作OE⊥AC于点E，连接FO，MO， ∵△ABC是边长为4的等边三角形，D为AB边的中点，以CD为直径画圆，
∴CD⊥AB，∠ACD=∠BCD=30°，AC=BC=AB=4，
∴∠FOD=∠DOM=60°，AD=BD=2，
∴CD=2 ，则CO=DO= ，
∴EO= ，EC=EF= ，则FC=3，
∴S△COF=S△COM= × ×3= ，
S扇形OFM= =π，
S△ABC= ×CD×4=4 ，
∴图中影阴部分的面积为：4 ﹣2× ﹣π=2.5 ﹣π．
故答案为：2.5 ﹣π．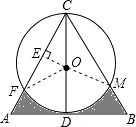

根据等边三角形的性质以及勾股定理得出△COF，△COM，△ABC以及扇形FOM的面积，进而得出答案．