题目内容
【题目】如图，直线y=x与双曲线y=
（k＞0，x＞0）交于点P，PA⊥x轴于点A，S△PAO=
（1）k= 点P的坐标为 ；
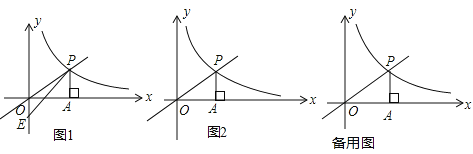
（2）如图1，点E的坐标为（0，﹣1），连接PE，过点P作PF⊥PE，交x轴于点F，求点F的坐标；
（3）如图2，将点A向右平移5个单位长度得点M，Q为双曲线y=
（x＞0）上一点且满足S△QPO=S△MPO，求点Q的坐标；
（4）将△PAO绕点P逆时针旋转一个角α（0°＜α＜180°），记旋转中的△PAO为△PA′O′设直线PO′、直线A′O′与x轴分别交于点G、H，是否存在这样的旋转角α，使得△GHO′为等腰三角形？若存在，直接写出α；若不存在，请说明理由．
【答案】（1）9，（3，3）（2）（7，0）（3）Q（9，1）或（1，9）；（4）当α为45°或67.5°或90°时，使△GHO′为等腰三角形
【解析】
试题分析：（1）由P为y=x与反比例函数的交点，得到P在y=x上，故设P（a，a），且a大于0，可得出AP=OA=a，由三角形AOP为直角三角形，且面积已知，利用三角形的面积公式列出关于a的方程，求出方程的解得到a的值，即可确定出P的坐标，将P的坐标代入反比例函数解析式中，即可求出k的值；
（2）根据题意过P作PF垂直于PE，交x轴于点F，过P作PB垂直于y轴于点B，先由一对对顶角相等及一对直角相等，利用三角形的内角和定理得出∠BEP=∠AFP，再由一对直角相等，以及BP=OA=AP，利用AAS可得出三角形BEP与三角形AFP全等，利用全等三角形的对应边相等可得出BE=AF，由OF=OA+AF，即可得出点F的坐标；
（3）连接OQ，PQ，过Q作QC⊥x轴于C点，由A的坐标及平移的规律找出M的坐标，在x轴上作出M点，连接PM，△POM以OM为底边，AP为高，求出△POM的面积，可得出△QPO的面积，由Q在反比例函数图象上，设出Q的坐标为Q（m，
）（m＞0），得出QC与OC，而△QOP的面积=△AOP的面积+直角梯形APQC的面积﹣△OQC的面积，而△AOP的面积与△QOC的面积相等，故△QOP的面积=直角梯形APQC的面积，由梯形的面积得出关于m的方程，求出方程的解得到m的值，即可得出Q的坐标；
（4）分三种情况分析讨论：①当GH=O′G时；②当GH=HO′时；③当GO′=HO′时；分别求得即可．
解：（1）由点P为y=x与反比例函数y=
的交点，设P（a，a）（a＞0），如图1所示：
可得出PA=OA=a，又S△PAO=
，
则
OA×PA=a2=
，
解得：a=3或a=﹣3（舍去），
则P（3，3），
将x=3，y=3代入反比例函数解析式得：3=
，
则k=3×3=9；
故答案为：9，（3，3）；
（2）过P作PF⊥PE，交x轴于点F，过P作PB⊥y轴于点B，如图2所示：
∴BP=AP=3，
∵∠ODE=∠PDF，∠EOD=∠EPF=90°，
∴∠BEP=∠AFP，
在△BEP和△AFP中，
，
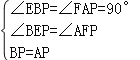∴△BEP≌△AFP（AAS），
∴BE=AF，
∵OA=PA=OB=3，点E的坐标为（0，﹣1），
∴BE=4，
∴OF=OA+AF=3+4=7，
∴点F的坐标为（7，0）；
（3）连接OQ，PQ，过Q作QC⊥x轴于C点，连接PM，如图3所示：
∵将A点沿x轴向右平移5个单位为M，
∴M（8，0），
∴OM=8，
∵PA=3，
∴S△MPO=
OM×PA=×8×3=12，
∵S△QPO=S△MPO，
∴S△QPO=12，
设Q（m，
）（m＞0），则有OC=m，QC=，
∵PA=OA=3，
∴AC=|m﹣3|，
∴S△QPO=S△PAO+S梯形APQC﹣S△QCO=
+
（
+3）|m﹣3|﹣=12，
整理得：（m﹣9）（m+1）=0或者（m+9）（m﹣1）=0，
解得：m=9或m=﹣1（舍去），或者m=1或m=﹣9（舍去），
∴Q（9，1）或（1，9）；
（4）分三种情况：
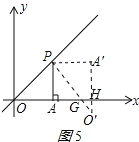
当GH=O′G时，如图4所示，
∵∠PO′A′=45°，
∴∠PO′A′=∠GHO′=45°，
∴∠O′GH=90°，
∴PO′⊥x轴
∴α=45°；
当GH=HO′时，如图5，∵∠PO′A′=45°，
∴∠PO′A′=∠HGO′=45°，
∴∠GHO′=90°，
∴A′O′⊥x轴，
∴α=90°；
当GO′=HO′时，如图6，
∵∠PO′A′=45°
∴∠GHO′=∠HGO′=67.5°，
∴∠PGA=67.5°，
∵∠PAG=90°，
∴∠APG=22.5°，
∵∠OPA=45°，
∴α=67.5°，
∴当α为45°或67.5°或90°时，使△GHO′为等腰三角形．
