题目内容
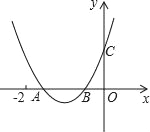
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2;②b2﹣4ac<4a2;③a>![]() ;其中正确的个数为( )
;其中正确的个数为( )
A. 0 B. 1 C. 2 D. 3
【答案】D
【解析】①∵OB=OC,
∴C(0,c),B(﹣c,0)
把B(﹣c,0)代入y=ax2+bx+c得0=ac2﹣bc+c,即0=ac2+c(1﹣b),
∵a>0,
∴1﹣b<0,即b>1,
如果b=2,由0=ac2﹣bc+c,可得ac=1,此是△=b2﹣4ac=0,故b>1且b≠2正确,
②∵a>0,b>0,c>0,设C(0,c),B(﹣c,0)
∵AB=|x1﹣x2|<2,
∴(x1+x2)2﹣4x1x2<4,
∴(﹣![]() )2﹣4×
)2﹣4×![]() <4,即
<4,即![]() ﹣
﹣![]() <4,
<4,
∴b2﹣4ac<4a2;故本项正确.
③把B(﹣c,0)代入y=ax2+bx+c可得ac+1=b,
代入y=ax2+bx+c得y=ax2+(ac+1)x+c=ax2+acx+x+c=ax2+x+acx+c=x(ax+1)+c(ax+1)=(x+c)(ax+1),
解得x1=﹣c,x2=﹣![]() ,
,
由图可得x1,x2>﹣2,
即﹣![]() >﹣2,
>﹣2,
∵a>0,
∴![]() <2,
<2,
∴a>![]() ;正确.
;正确.
所以正确的个数是3个.
故选:D.

练习册系列答案
相关题目