题目内容
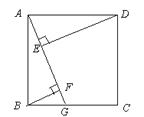
【题目】如图,四边形ABCD是正方形, 点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F.
(1) 求证:DE-BF = EF;
(2) 当点G为BC边中点时, 试探究线段EF与GF之间的数量关系,并说明理由.
【答案】(1)证明见解析;(2)EF = 2FG,理由见解析.
【解析】分析:(1)本题的关键是求△ADE≌△ABF,以此来得出DE=AF=AE+EF=BE+EF,这两个三角形中已知的条件有AD=BA,一组直角,关键是再找出一组对应角相等,可通过证明∠DAF和∠ABF来实现.(通过平行和等角的余角相等来证得)
(2)通过证明△AFB ∽△BFG ∽△ABG,得出AB,BG;AF,BF;BF,BG之间的比例关系,根据点G为BC边中点,来得出AF,BF,BF,FG之间的比例关系,然后根据(1)中得出的结果来求BF,FG的大小关系.
详解:(1) 证明:
∵ 四边形ABCD 是正方形, BF⊥AG , DE⊥AG
∴ DA=AB, ∠BAF + ∠DAE = ∠DAE + ∠ADE = 90°
∴ ∠BAF = ∠ADE ∴ △ABF ≌ △DAE
∴ BF = AE , AF = DE
∴ DE-BF = AF-AE = EF
(2)EF = 2FG 理由如下:
∵ AB⊥BC , BF⊥AG , AB =2 BG
∴ △AFB ∽△BFG ∽△ABG
∴![]()
∴ AF = 2BF , BF =2FG
由(1)知, AE = BF,∴ EF = BF = 2 FG

练习册系列答案
相关题目