��Ŀ����
����Ŀ��Ϊ��һ������·��·ò���������߹�·�����ȣ�ij����ز��ų����ⶨ��һ�����̶Ӷ�һ�γ��Ȳ�����39000�Ĺ�·����·���������ޣ��ù��̶��Ծ��豸�����豸����ʹ�õķ�ʽʩ����ԭ�ƻ����豸ÿСʱ����·30�ף����豸ÿСʱ����·60��
��1�����ڱ������豸��Ŀ�ģ��ù��̶Ӽƻ�ʹ�����豸��ʱ���ʹ�þ��豸��ʱ���![]() ������������깤ʱ�����豸��ʹ��ʱ������Ϊ����Сʱ��
������������깤ʱ�����豸��ʹ��ʱ������Ϊ����Сʱ��
��2��ͨ����ȷ�Ŀ��졢��������滮���Լ������˲���֧�߹�·���ޣ��˹��̵�ʵ��ʩ����̱�����ⶨ���������39000����9000�ף�������ʵ��ʩ���У����豸������·Ч�ʲ��������£�ʹ��ʱ��ȣ�1���е���Сֵ��![]() ��ͬʱ����Ϊ���˲������豸����������ʹ�õ����豸����·��Ч�ʱ�ԭ�ƻ��½���
��ͬʱ����Ϊ���˲������豸����������ʹ�õ����豸����·��Ч�ʱ�ԭ�ƻ��½���![]() ��ʹ��ʱ��ȣ�1�������豸ʹ�õ����ʱ���
��ʹ��ʱ��ȣ�1�������豸ʹ�õ����ʱ���![]() ����
����![]() ��ֵ��
��ֵ��
���𰸡���1��300 ��2��32
��������
��1��������������깤ʱ���豸��ʹ��ʱ������ΪxСʱ�����������ҵ����������ϵ��ʹ�����豸���Ĺ�·������ʹ�þ��豸���Ĺ�·�����ĺͲ�����39000�ף��г�����ʽ���ⲻ��ʽ���ɣ�
��2�����������֪����ʵ��ʩ����ʹ�þ��豸��ʱ��Ϊ300��(1+3.2![]() %)Сʱ��ÿСʱ����·30�ף�ʹ�����豸��ʱ��Ϊ300
%)Сʱ��ÿСʱ����·30�ף�ʹ�����豸��ʱ��Ϊ300![]() (1-
(1-![]()
![]() %-30%)Сʱ��ÿСʱ����·60��(1-
%-30%)Сʱ��ÿСʱ����·60��(1-![]() %)�ף���ʵ��ʩ����ʹ�����豸���Ĺ�·����Ϊ300��(1+3.2
%)�ף���ʵ��ʩ����ʹ�����豸���Ĺ�·����Ϊ300��(1+3.2![]() %)��30����ʹ�þ��豸��������60��(1-
%)��30����ʹ�þ��豸��������60��(1-![]() %)��300
%)��300![]() (1-
(1-![]()
![]() %-30%)��������·�����������������������ϵ�г����̣�����⼴�ɣ�
%-30%)��������·�����������������������ϵ�г����̣�����⼴�ɣ�
�⣺����������깤ʱ�����豸��ʹ��ʱ������ΪxСʱ,�����豸��ʹ��ʱ��Ϊ![]() Сʱ�����������
Сʱ�����������
![]()
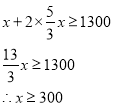
�𣺵���������깤ʱ�����豸��ʹ��ʱ������Ϊ300Сʱ
��2���������
300��(1+3.2![]() %)��30+60��(1-
%)��30+60��(1-![]() %)��300
%)��300![]() �� (1+
�� (1+![]()
![]() %+30%)=39000+9000
%+30%)=39000+9000
ԭ���̻����![]()
���![]() ��
��![]() ��
��
��![]() ��0
��0
��![]() =
=![]()
��![]() ��ֵ��
��ֵ��![]()

 ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�
ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�