题目内容
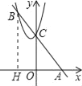
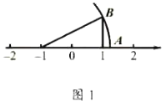
【题目】(1)如图1,![]() 中,
中,![]() ,点
,点![]() 在数轴-1处,点
在数轴-1处,点![]() 在数轴1处,
在数轴1处,![]() ,
,![]() ,则数轴上点
,则数轴上点![]() 对应的数是 .
对应的数是 .
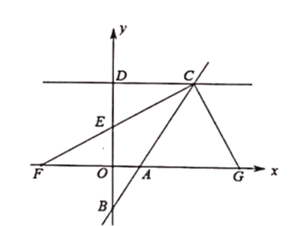
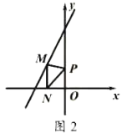
(2)如图2,点![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,点
,点![]() 是
是![]() 轴上的动点,当以
轴上的动点,当以![]() ,
,![]() ,
,![]() 为顶点的三角形为等腰直角三角形时点
为顶点的三角形为等腰直角三角形时点![]() 的坐标为 .
的坐标为 .
【答案】(1)![]() ;(2)M坐标是(-3,-3),(-1,1),(
;(2)M坐标是(-3,-3),(-1,1),(![]() ,
,![]() ).
).
【解析】
(1)通过勾股定理求出线段MB,而线段MA=MB,进而知道点A对应的数,减去1即可得出答案.
(2)分四种情况考虑:当M运动到(-1,1)时,ON=1,MN=1,由MN⊥x轴,以及ON=MN;又当M运动到第三象限时,要MN=MP,且PM⊥MN时;若MN为斜边时,则∠ONP=45°,所以ON=OP,求出此时M坐标;又当点M′在第二象限,M′N′为斜边时,这时N′P=M′P,∠M′N′P=45°,求出此时M坐标,综上,得到所有满足题意M的坐标.
解:在Rt△MBC中,∠MCB=90°,
∴![]()
∴![]() ,
,
∵MA=MB,
∴![]() ,
,
∵点M在数轴-1处,
∴数轴上点A对应的数是![]() ;
;
(2)①如图1,
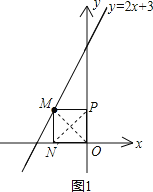
当M运动到(-1,1)时,ON=1,MN=1,
∵MN⊥x轴,所以由ON=MN可知,△MNP为等腰直角三角形;
②如图2,
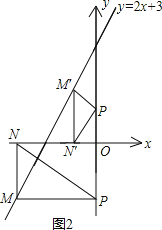
当M运动到第三象限时,要MN=MP,且PM⊥MN,
设点M(x,2x+3),则有:-x=-(2x+3),
解得:x=-3,
所以点M坐标为(-3,-3).
若MN为斜边时,则∠ONP=45°,所以ON=OP,设点M(x,2x+3),
则有![]() ,化简得-2x=-2x-3,
,化简得-2x=-2x-3,
这方程无解,所以这时不存在符合条件的M点;
③如图2,
∵当点M′在第二象限,M′N′为斜边时,这时N′P=M′P,∠M′N′P=45°,
设点M′(x,2x+3),则OP=ON′,而![]() ,
,
∴有![]() ,
,
解得:![]() ,
,
∴M′(![]() ,
,![]() ),
),
综上,符合条件的点M坐标是(-3,-3),(-1,1),(![]() ,
,![]() ).
).