Question

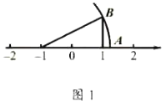
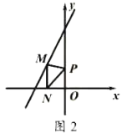
【题目】如图，直角坐标系中，直线分别与轴、轴交于点，点，过作平行轴的直线，交于点，点在线段上，延长交轴于点，点在轴正半轴上，且．

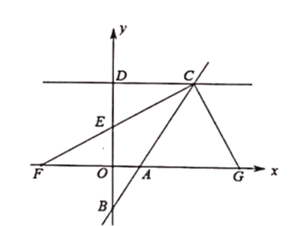
（1）求直线的函数表达式．

（2）当点恰好是中点时，求的面积．

（3）是否存在，使得是直角三角形？若存在，直接写出的值;若不存在，请说明理由．

Answer 1

【答案】（1）；（2）48；（3）存在，或

【解析】

（1）将A，B两点坐标代入中求出k，b即可得解；

（2）根据题意，过点作轴于点，分别求出和的长即可得到的面积；

（3）根据题意进行分类讨论，分别为CF⊥CG时和CF⊥x轴时，进而求出F点坐标得到直线的解析式即可得解.

（1）将点，点代入直线得；

（2）当时，

解得

点的坐标为

∴

是中点，

易得

∵

∴

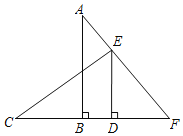
如下图所示，过点作轴于点

∴；

（3）存在使得是直角三角形

当CF⊥CG时

∵

∴

∵，

∴

∴

∴直线得解析式为：

∴

∴；

当CF⊥x轴时

∵

∴

∵，

∴

∴直线得解析式为：

∴

∴；

综上所述：∴或.