题目内容
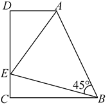
【题目】如图,在梯形ABCD中,AD∥BC(BC>AD),∠D=90°,BC=CD=12,∠ABE=45°,若AE=10.求CE的长度.
【答案】CE的长为4或6.
【解析】
过B作DA的垂线交DA的延长线于M,M为垂足,延长DM到G,使MG=CE,连接BG.求证△BEC≌△BMG,△ABE≌△ABG,设CE=x,在直角△ADE中,根据AE2=AD2+DE2求x的值,可以求CE的长度.
过B作DA的垂线交DA的延长线于M,M为垂足,
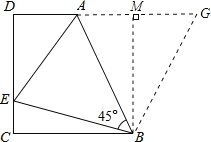
延长DM到G,使MG=CE,连接BG,
易知四边形BCDM是正方形,
则△BEC与△BGM中,
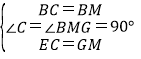 ,
,
∴△BEC≌△BMG(SAS),
∴∠MBG=∠CBE,BE=BG,
∵∠ABE=45°,
∴∠CBE+∠ABM=∠MBG+∠ABM=45°,
即∠ABE=∠ABG=45°,
在△ABE与△ABG中,
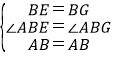 ,
,
∴△ABE≌△ABG(SAS),
∴AG=AE=10,
设CE=x,则AM=10-x,
AD=12-(10-x)=2+x,DE=12-x,
在Rt△ADE中,AE2=AD2+DE2,
∴100=(x+2)2+(12-x)2,
即x2-10x+24=0;
解得:x1=4,x2=6.
故CE的长为4或6.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案【题目】(本小题满分7分) 已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=![]() OB.
OB.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.

【题目】抛物线![]() 上部分点的横坐标x,纵坐标y的对应值如下表:
上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为(﹣2,0);②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是x=1;④在对称轴左侧y随x增大而增大.
A. 1 B. 2 C. 3 D. 4





