题目内容
【题目】如图1,在平面直角坐标系中,直线AB与x轴交于点A(m,0),与y轴交于点B(0,n),且m,n满足:(m+n)2+|n﹣6|=0.

(1)求:①m,n的值;②S△ABO的值;
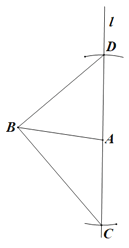
(2)D为OA延长线上一动点,以BD为直角边作等腰直角△BDE,连接EA,求直线EA与y轴交点F的坐标.
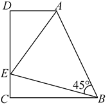
(3)如图2,点E为y轴正半轴上一点,且∠OAE=30°,AF平分∠OAE,点M是射线AF上一动点,点N是线段OA上一动点,试求OM+MN的最小值(图1与图2中点A的坐标相同).
【答案】(1)①m=﹣6,n=6,②18;(2)F(0,﹣6);(3)OM+MN的最小值为3.
【解析】
(1)①利用非负数的性质即可解决问题.
②先确定出OA=OB=6,从而求得△ABO的面积.
(2)先判断出△DEM≌△BDO得出EM=DO,MD=OB=OA=6,进而判断出AM=EM,即可得出∠OAF=45°,即可得出点F坐标,最后用待定系数法得出直线EA解析式.
(3)过点O作OG⊥AE于G,交AF于M,作MN⊥OA于N,连接MN,此时OM+MN的值最小.
(1)①∵(m+n)2+|n﹣6|=0,
又∵(m+n)2≥0,|n﹣6|≥0.
∴m+n=0,n=6,
∴m=﹣6,n=6.
②∵直线AB与x轴交于点A(﹣6,0),与y轴交于B(0,6).
∴OA=6,OB=6,
∴S△ABO=![]() OAOB=
OAOB=![]() ×6×6=18;
×6×6=18;
(2)如图1,过点E作EM⊥x轴于M,
∴∠MDE+∠DEM=90°,
∵△BDE是等腰直角三角形,
∴DE=DB,∠BDE=90°,
∴∠MDE+∠BDO=90°,
∴∠DEM=∠BDO,
在△DEM和△BDO中,
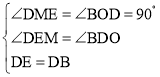 ,
,
∴△DEM≌△BDO(AAS),
∴EM=DO,MD=OB=OA=6,
∴AM=DM+AD=6+AD,
EM=OD=OA+AD=6+AD,
∴EM=AM,
∴∠MAE=45°=∠OAF,
∴OA=OF,
∴F(0,﹣6).
(3)如图2中,

过点O作OG⊥AE于G,交AF于M,作MN⊥OA于N,连接MN,此时OM+MN的值最小.
∵∠MAG=∠MAN,MG⊥AG,MN⊥AN,
∴MG=MN,
∴OM+MN=OM+MG=OG,
在Rt△OAG中,∠OAE=30°,OA=6,
∴OG=3,
∴OM+MN的最小值为3.