题目内容
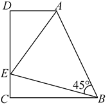
【题目】如图的实线部分是由 Rt△ABC 经过两次折叠得到的,首先将 Rt△ABC 沿 BD 折叠,使点 C落在斜边上的点 C′处,再沿 DE 折叠,使点 A 落在 DC′的延长线上的点 A′处.若图中∠C=90°,DE=3cm,BD=4cm,则 DC′的长为_____.

【答案】![]() cm.
cm.
【解析】
根据折叠的性质可得∠B C′D=∠C=90°,DB和DE分别是∠CDC′和∠ADA′的角平分线,可求得∠BDE=90°,在直角△BDE中利用勾股定理求得BE的长,再根据三角形的面积即可求解.
解:由折叠可知,∠B C′D=∠C=90°,∠ADE=∠ A′DE,∠BDC=∠BDC′,
又∵∠ADE+∠ A′DE+ BDC+∠BDC′=180°,
∴∠BDE=90°,
在直角△BDE中,DE=3cm,BD=4cm,
∴BE=![]() =
=![]() =5 cm,
=5 cm,
∵∠B C′D=90°,
∴![]()
即4×3=5 DC′, DC′=![]() cm.
cm.
故答案为:![]() cm.
cm.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目