��Ŀ����
12����֪����P��ƽ���ı���ABCD�Խ���AC����ֱ���ϵ�һ�����㣨��P�����A��C�غϣ����ֱ����A��C��ֱ��BP�����ߣ�����ֱ�Ϊ��E��F����OΪAC���е㣮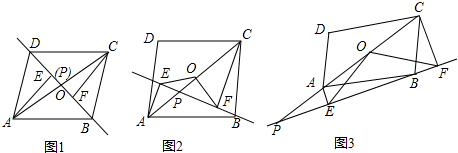
��1������P���O�غ�ʱ����ͼ1��˵����OE=OF
��2����ֱ��BP�Ƶ�B��ʱ�뷽����ת����P�ڶԽ���AC�ϣ�����ͼ2����1���еĽ����Ƿ������˵�����ɣ�
��3��ֱ��BP�Ƶ�B��ʱ�뷽����תͼ3��λ�ã���P�ڶԽ���AC���ӳ����ϣ�������OFE=30�㣬�����߶�CF��AE��OE֮����������������ϵ��
���� ��1��֤����AOE�ա�COF���ɵó����ۣ�
��2����1���еĽ�����Ȼ�������������ߣ�����ȫ�������Σ�֤����AOE�ա�CGO����OE=OG���ٸ���ֱ��������б���ϵ����ߵ���б�ߵ�һ��ó����ۣ�
��3��FC+AE=OE�������ǣ��������ߣ�����ȫ�������Σ��루2�����ƣ�ͬ���ã���AOE�ա�COG��OF=$\frac{1}{2}$EG=OE=OG�������á�OFE=30�㣬�á�GOF�ǵȱ������Σ����ݱ߳���ȿ��Եó����ۣ�
��� �⣺��1����ͼ1�����ı���ABCD��ƽ���ı��Σ�
��OA=OC��
��AE��BP��CF��BP��
���AEO=��CFO=90�㣬
�ߡ�AOE=��COF��
���AOE�ա�COF��AAS����
��OE=OF��
��2����ͼ2����1���еĽ�����Ȼ�����������ǣ�
�ӳ�EO��CF��G��
��AE��BP��CF��BP��
��AE��CF��
���EAO=��OCG��
��AO=OC����AOE=��COG��
���AOE�ա�COG��
��EO=OG��
��Rt��EFG��FO=$\frac{1}{2}$EG=OE��
��3��FC+AE=OE�������ǣ�
��ͼ3���ӳ�EO��FC����G��
ͬ���ã���AOE�ա�COG��
��OE=OG��AE=CG��
��Rt��EGF��OF=$\frac{1}{2}$EG=OE=OG��
�ߡ�OFE=30�㣬
���OEF=��OFE=30�㣬
���GOF=60�㣬
���GOF�ǵȱ������Σ�
��FG=OG��
��FC+CG=OG��
��FC+AE=OE��
���� ���⿼����ƽ���ı��Ρ�ȫ�������ε����ʺ��ж��Լ����������ε����ʺ��ж����Թ���ȫ�������κ�֤��������ȫ����ͻ�ƿڣ�����ƽ���ı��εĶԽ�����ƽ�ֵ�ȫ�ȵı���ȵ��������Ӷ�ʹ������Խ����

| A�� | ��a-1����a+1�� | B�� | ��3+a����a-3�� | C�� | ��a+2b����2a-b�� | D�� | ��-2+b����-2-b�� |
| A�� | ֱ�������� | B�� | �߶� | C�� | �� | D�� | �������� |
| A�� | 10.6��104 | B�� | 10.6��106 | C�� | 106��103 | D�� | 1.06��105 |
| A�� | $\frac{1}{4}$��$\frac{1}{16}$ | B�� | $\frac{1}{2}$��$\frac{1}{8}$ | C�� | $\frac{1}{4}$��$\frac{1}{8}$ | D�� | $\frac{1}{2}$��$\frac{1}{16}$ |
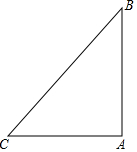 ��ͼ����֪��ABC�У���BAC=90�㣬AB=AC����D�ǡ�ABC�ڵ�һ�㣬��AD=CD��BD=BA��
��ͼ����֪��ABC�У���BAC=90�㣬AB=AC����D�ǡ�ABC�ڵ�һ�㣬��AD=CD��BD=BA��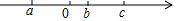 ��֪������a��b��c�������ϵ�λ����ͼ��ʾ������2��a+b��-3|a-c|+2|c-b|
��֪������a��b��c�������ϵ�λ����ͼ��ʾ������2��a+b��-3|a-c|+2|c-b|