题目内容
【题目】如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,BE=DF,在此图中是否存在两个全等的三角形,并说明理由;它们能够由其中一个通过旋转而得到另外一个吗?简述旋转过程.

【答案】在此图中存在两个全等的三角形,即△CDF≌△CBE.△CDF是由△CBE绕点C沿顺时针方向旋转90°得到的.理由见解析.
【解析】
在△CDF和△CBE中,根据正方形的性质知DC=BC、已知条件DF=BE可以证得△CDF≌△CBF.
解:在此图中存在两个全等的三角形,即△CDF≌△CBE.理由如下:
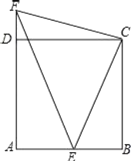
∵点F在正方形ABCD的边AD的延长线上,
∴∠CDF=∠CDA=90°;
在△CDF和△CBE中,
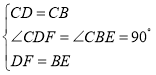 ,
,
∴△CDF≌△CBE(SAS),
∴∠FCD=∠ECB,CF=CE,
∴∠FCE=∠FCD+∠DCE=∠ECB+∠DCE=∠DCB=90°,
∴△CDF是由△CBE绕点C沿顺时针方向旋转90°得到的.

练习册系列答案
相关题目
【题目】某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了尚不完整的统计图表(如图),并计算了甲成绩的平均数和方差(见如图小宇的作业).
甲、乙两人射箭成绩统计表
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 7 | a | 7 |

(1)a= ;
(2)请完成图中表示乙成绩变化情况的折线.
(3)观察图,可看出 的成绩比较稳定(填“甲”或“乙”).参照小宇的计算方法,计算乙成绩的方差,并验证你的判断.


