题目内容
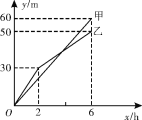
【题目】某批发市场批发甲、乙两种水果，根据以往经验和市场行情，预计夏季某一段时间内，甲种水果的销售利润
(万元)与进货量
(t)近似满足函数关系
;乙种水果的销售利润
(万元)与进货量
(t)近似满足函数关系
(其中
， 
、
为常数)，且进货量
为1t时，销售利润
为1. 4万元;进货量
为2t时，销售利润
为2. 6万元.
(1)求
(万元)与
(t)之间的函数关系式;
(2)如果市场准备进甲、乙两种水果共10t，设乙种水果的进货量为
(t)，请你写出这两种水果所获得的销售利润之和
(万元)与
(t)之间的函数关系式.并求出这两种水果各进多少吨时获得的销售利润之和最大，最大利润是多少.
【答案】（1）
（2）甲、乙两种水果的进货量分别为4t和6t时，获得的销售利润之和最大，最大利润是6. 6万元
【解析】试题分析：（1）根据题意列出二元一次方程组，求出a、b的值即可求出函数关系式的解．
（2）已知w=y甲+y乙=0.3（10﹣t）+（﹣0.1t2+1.5t），用配方法化简函数关系式即可求出w的最大值．
试题解析：解： （1）由题意，得
．
解得
．
所以
．
（2）由题意，得： 
，
所以
，
即当
时， 
有最大值为6.6．
所以
（t）．
答：甲种水果的进货量为4t，乙种水果的进货量为6t时，获得的销售利润之和最大，最大利润是6.6万元．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
