题目内容
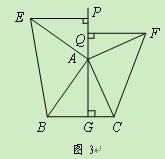
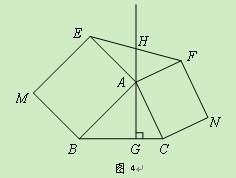
【题目】有一块形状如图的五边形余料![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .要在这块余料中截取一块矩形材料,其中一边在
.要在这块余料中截取一块矩形材料,其中一边在![]() 上,并使所截矩形的面积尽可能大.
上,并使所截矩形的面积尽可能大.
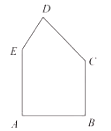
(1)若所截矩形材料的一条边是![]() 或
或![]() ,求矩形材料的面积;
,求矩形材料的面积;
(2)能否截出比(1)中面积更大的矩形材料?如果能,求出这些矩形材料面积的最大值,如果不能,请说明理由.
【答案】(1)S=30;(2)能,![]() 的最大值为30.25.
的最大值为30.25.
【解析】
(1)①若所截矩形材料的一条边是BC,过点C作CF⊥AE于F,得出S1=ABBC=6×5=30;
②若所截矩形材料的一条边是AE,过点E作EF∥AB交CD于F,FG⊥AB于G,过点C作CH⊥FG于H,则四边形AEFG为矩形,四边形BCHG为矩形,证出△CHF为等腰三角形,得出AE=FG=6,HG=BC=5,BG=CH=FH,求出BG=CH=FH=FG-HG=1,AG=AB-BG=5,得出S2=AEAG=6×5=30;
(2)在CD上取点F,过点F作FM⊥AB于M,FN⊥AE于N,过点C作CG⊥FM于G,则四边形ANFM为矩形,四边形BCGM为矩形,证出△CGF为等腰三角形,得出MG=BC=5,BM=CG,FG=DG,设AM=x,则BM=6-x,FM=GM+FG=GM+CG=BC+BM=11-x,得出S=AM×FM=x(11-x)=-x2+11x,由二次函数的性质即可得出结果.
(1)①若所截矩形材料的一条边是BC,如图1所示:
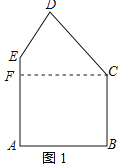
过点C作CF⊥AE于F,S1=ABBC=6×5=30;
②若所截矩形材料的一条边是AE,如图2所示:
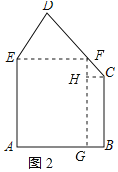
过点E作EF∥AB交CD于F,FG⊥AB于G,过点C作CH⊥FG于H,
则四边形AEFG为矩形,四边形BCHG为矩形,
∵∠C=135°,
∴∠FCH=45°,
∴△CHF为等腰直角三角形,
∴AE=FG=6,HG=BC=5,BG=CH=FH,
∴BG=CH=FH=FG-HG=6-5=1,
∴AG=AB-BG=6-1=5,
∴S2=AEAG=6×5=30;
(2)能;理由如下:
在CD上取点F,过点F作FM⊥AB于M,FN⊥AE于N,过点C作CG⊥FM于G,
则四边形ANFM为矩形,四边形BCGM为矩形,
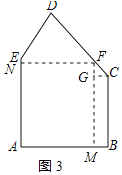
∵∠C=135°,
∴∠FCG=45°,
∴△CGF为等腰直角三角形,
∴MG=BC=5,BM=CG,FG=DG,
设AM=x,则BM=6-x,
∴FM=GM+FG=GM+CG=BC+BM=11-x,
∴S=AM×FM=x(11-x)=-x2+11x=-(x-5.5)2+30.25,
∴当x=5.5时,S的最大值为30.25.