��Ŀ����
����Ŀ���������֣���ͼ����֪��ABC����ADE��Ϊ���������Σ�AB��AC��AD��AE���������������η�����һ��ʹ��B��D��E��ͬһֱ���ϣ�����CE��

��1����ͼ1������ABC����ACB����ADE����AED��55������֤����BAD�ա�CAE��
��2���ڣ�1���������£����BEC�Ķ�����
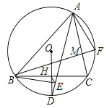
�ع�̽������3����ͼ2������CAB����EAD��120����BD��4��CFΪ��BCE��BE���ϵĸߣ���ֱ��д��EF�ij��ȣ�
���𰸡���1������������2��70������3��2
��������
��1������SAS֤����BAD�ա�CAE���ɣ�
��2������ȫ�������ε����ʽ�����⼴�ɣ�
��3��ͬ����֤��BAD�ա�CAE���Ƴ�EC=BD=4���ɡ�BEC=��BAC=120�����Ƴ���FCE=30�����ɽ�����⣮
��1��֤������ͼ1�У�
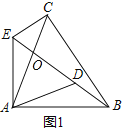
�ߡ�ABC����ACB����ADE����AED��
���EAD����CAB��
���EAC����DAB��
��AE��AD��AC��AB��
���BAD�ա�CAE��SAS����
��2���⣺��ͼ1�У���AC��BE��O��
�ߡ�ABC����ACB��55����
���BAC��180����110����70����
�ߡ�BAD�ա�CAE��
���ABO����ECO��
�ߡ�EOC����AOB��
���CEO����BAO��70����
����BEC��70����
��3���⣺��ͼ2�У�

�ߡ�CAB����EAD��120����
���BAD����CAE��
��AB��AC��AD��AE��
���BAD�ա�CAE��SAS����
���BAD����ACE��BD��EC��4��
ͬ����֤��BEC����BAC��120����
���FEC��60����
��CF��EF��
���F��90����
���FCE��30����
��EF��![]() EC��2.
EC��2.

����Ŀ��Ϊ���Ϳ�����Ⱦ��������˾����ȫ���������ܻ�����ȼ�����������ƻ�����A�ͺ�B�����ֹ�������10��������ÿ̨�ļ۸�����ؿ��������
A�� | B�� | |
�۸���Ԫ/���� | a | b |
����ؿ���������/��/���� | 60 | 100 |
������A������1����B������2��������400��Ԫ��������A������2����B������1��������350��Ԫ
��1������ÿ��A��������ÿ��B�������ֱ������Ԫ��
��2������ù�˾����A�ͺ�B���������ܷ��ò�����1200��Ԫ����ȷ����10������������ؿ��ܺͲ�����680���˴Σ����ļ��ֹ����������������һ��������ʹ�ù����ܷ������٣�