题目内容
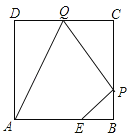
【题目】如图，已知四边形ABCD是矩形，把矩形沿直线AC折叠，点B落在点E处，
（1）求证：△AOE≌△COD；
（2）连接DE，若DE：AC＝3：5，求tan∠ACB．
【答案】（1）见解析；（2）
【解析】
（1）由矩形的性质和折叠的性质可得AE=CD，由“AAS”可证△AEO≌△CDO；
（2）由全等三角形的性质可得AO=CO，EO=DO，即可得
，可证△DOE∽△COA，可得EO：CO=3：5，即可设EO=DO=3x，AO=CO=5x，AD=8x，由勾股定理可求CD=4x=AB，即可求解．
解：证明：（1）∵四边形ABCD是矩形
∴AB＝CD，AD＝BC，∠B＝∠ADC＝90°，
∵折叠
∴AE＝AB，
∵AE＝CD，∠AOE＝∠COD，∠AEC＝∠ADC
∴△AEO≌△CDO（AAS）
（2）∵△AEO≌△CDO
∴AO＝CO，EO＝DO
∴且∠AOC＝∠DOE
∴△DOE∽△COA
∴
，且DE：AC＝3：5，
∴EO：CO＝3：5
设EO＝DO＝3x，AO＝CO＝5x，
∴DA＝BC＝8x，CD＝
＝4x＝AB
∴tan∠ACB＝
＝
＝
练习册系列答案
相关题目
