题目内容
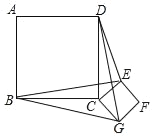
【题目】在等腰三角形ABC中,∠ABC=90度,D是AC边上的动点,连结BD,E、F分别是AB、BC上的点,且DE⊥DF.、(1)如图1,若D为AC边上的中点.
(1)填空:∠C= ,∠DBC= ;
(2)求证:△BDE≌△CDF.
(3)如图2,D从点C出发,点E在PD上,以每秒1个单位的速度向终点A运动,过点B作BP∥AC,且PB=AC=4,点E在PD上,设点D运动的时间为t秒(0≤1≤4)在点D运动的过程中,图中能否出现全等三角形?若能,请直接写出t的值以及所对应的全等三角形的对数,若不能,请说明理由.

【答案】(1)45°,45°;(2)见解析;(3)当t=0时,△PBE≌△CAE一对,当t=2时,△AED≌△BFD,△ABD≌△CBD,△BED≌△CFD共三对,当t=4时,△PBA≌△CAB一对.
【解析】
(1)利用等腰直角三角形的性质得出答案;
(2)利用等腰直角三角形的性质结合ASA进而得出答案;
(3)当t=0时,t=2时,t=4时分别作出图形,得出答案.
(1)解:∵在等腰三角形ABC中,∠ABC=90度,D为AC边上的中点,
∴∠C=45°,BD⊥AC,
∴∠DBC=45°;
故答案为:45°;45°;
(2)证明:在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,
∴BD⊥AC,
又∵ED⊥DF,
∴∠BDE+∠BDF=∠CDF+∠BDF=90°,
∴∠BDE=∠CDF,
∵∠C=∠DBC=45°,
∴BD=DC,∠EBD=90°-∠DBC=45°,
在△BDE和△CDF中,
 ,
,
∴△BDE≌△CDF(ASA);
(3)解:如图①所示:当t=0时,△PBE≌△CAE一对;

理由:∵BP∥AC
∴∠P=∠ACE
在△PBE和△CAE中,

∴△PBE≌△CAE(AAS)
如图②所示:当t=2时,△AED≌△BFD,△ABD≌△CBD,△BED≌△CFD共三对;

理由:在△ABD和△CBD中,

∴△ABD≌△CBD(SSS)
由(2)可知∠ADE+∠BDE=∠BDF+∠BDE,
∴∠ADE=∠BDF
在△AED和△BFD中,

∴△AED≌△BFD(ASA)
同理可证△BED≌△CFD.
如图③所示:当t=4时,△PBA≌△CAB一对.

理由:∵PB∥AC,
∴∠PBA=∠CAB,
在△PBA和△CAB中,

∴△PBA≌△CAB(SAS)
综上所述,答案为:
当t=0时,△PBE≌△CAE一对,当t=2时,△AED≌△BFD,△ABD≌△CBD,△BED≌△CFD共三对,当t=4时,△PBA≌△CAB一对.

 名校课堂系列答案
名校课堂系列答案