题目内容
【题目】已知,在Rt△ABC中,∠C=90°,AC=15,BC=8,D为AB的中点,E点在边AC上,将△BDE沿DE折叠得到△B1DE,若△B1DE与△ADE重叠部分面积为△ADE面积的一半,则CE=_____________.
【答案】![]() 或
或![]()
【解析】
分两种情形:①如图1中,设AD交EB1于O,当DO=OA时,△B1DE与△ADE重叠部分面积为△ADE面积的一半.②:如图2中,当DB1平分线段AE时,满足条件.分别求解即可解决问题;
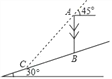
情形1:如图1中,设AD交EB1于O,当DO=OA时,△B1DE与△ADE重叠部分面积为△ADE面积的一半.

作DM⊥BE于M,DN⊥EB1于N.
∵BC=8,AC=15,∠C=90°,
∴AB=![]() =17,
=17,
∵D是AB中点,
∴BD=AD=![]() ,
,
∵∠BED=∠DEB1,
∴DM=DN,
∵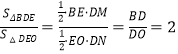 ,
,
∴BE=2EO,
∵BE=EB1,
∴EO=OB1,∵DO=OA,
∴四边形DEAB1是平行四边形,
∴DB1=BD=AE=![]() ,
,
∴CE=AC﹣AE=![]()
情形2:如图2中,当DB1平分线段AE时,满足条件.

∵BD=AD,EO=OA,
∴OD∥BE,
∴∠BED=∠EDO=∠BDE,
∴BE=BD=![]() ,
,
在Rt△BCE中,EC=![]() .
.
综上所述,满足条件的CE的值为![]() 或
或![]() .
.
故答案是:![]() 或
或![]() .
.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目