题目内容
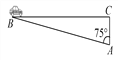
【题目】如图,⊙O中,点A为弧BC中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
(1)求证:PA是⊙O的切线;
(2)若BC=2![]() ,AB=2
,AB=2![]() ,求sin∠ABD的值.
,求sin∠ABD的值.

【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)根据垂径定理得出AO⊥BC,进而根据平行线的性质得出AP⊥AO,即可证得结论;
(2)根据垂径定理得出BE=![]() ,在RT△ABE中,利用锐角三角函数关系得出sin∠BAO=
,在RT△ABE中,利用锐角三角函数关系得出sin∠BAO=![]() ,再根据等腰三角形的性质得出∠ABD=∠BAO,即可求得求sin∠ABD=sin∠BAO=
,再根据等腰三角形的性质得出∠ABD=∠BAO,即可求得求sin∠ABD=sin∠BAO=![]() .
.
(1)证明:连结AO,交BC于点E.
∵点A是![]() 的中点
的中点
∴AO⊥BC,
又∵AP∥BC,
∴AP⊥AO,
∴AP是⊙O的切线;
(2)解:∵AO⊥BC,BC=2![]() ,
,
∴BE=![]() ,
,
又∵AB=6
∴sin∠BAE=![]() =
=![]() ,
,
∵OA=OB
∴∠ABD=∠BAO,
∴sin∠ABD=sin∠BAE=![]() .
.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
【题目】某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了尚不完整的统计图表(如图),并计算了甲成绩的平均数和方差(见如图小宇的作业).
甲、乙两人射箭成绩统计表
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 7 | a | 7 |

(1)a= ;
(2)请完成图中表示乙成绩变化情况的折线.
(3)观察图,可看出 的成绩比较稳定(填“甲”或“乙”).参照小宇的计算方法,计算乙成绩的方差,并验证你的判断.