题目内容
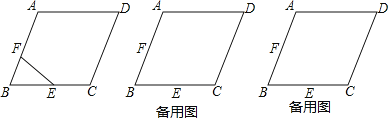
【题目】在△ABC中,点D在边BC上,点E在线段AD上.
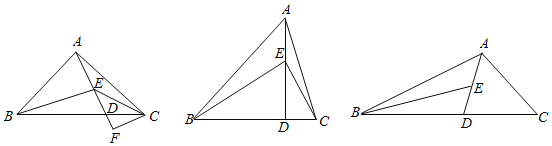
(1)若∠BAC=∠BED=2∠CED=α,
①若α=90°,AB=AC,过C作CF⊥AD于点F,求![]() 的值;
的值;
②若BD=3CD,求![]() 的值;
的值;
(2)AD为△ABC的角平分线,AE=ED=2,AC=5,tan∠BED=2,直接写出BE的长度.
【答案】(1)①2;②![]() ;(2)
;(2)![]()
【解析】
(1)①由题意先判定△ABC与△CEF都是等腰直角三角形,再判定△ABE≌△CAF(AAS),则可由全等三角形的性质及中线的定义可得答案;②过点C作CF∥BE,交AD的延长线于点F,在AD上取一点G,使得CG=CF,由两组角对应相等判定△ABE∽△CAG,再由CF∥BE判定△BED∽△CFD,由相似三角形的性质得两个比例等式,设CF=x,BE=3x,AE=y,则CG=EG=x,代入比例式化简计算可得答案.
(2)过点C作CF∥AD,交BA的延长线于F,延长BE交CF与G,利用等腰三角形的判定与性质进行推理,结合tan∠BED=2,得出AG的长;利用勾股数得出FG与CG的长;由DE∥CG得出比例式,计算可求得BE的长.
解:(1)①∵∠BAC=∠BED=2∠CED=α,
∴当α=90°,AB=AC时,△ABC与△CEF都是等腰直角三角形,
∴∠BAE+∠FAC=90°,∠ACF+∠FAC=90°,
∴∠BAE=∠AFC,
∴在△ABE与△CAF中,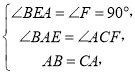
∴△ABE≌△CAF(AAS),
∴AE=CF=EF,
∴BE=AF=2EF=2CF,
∴![]() =2;
=2;
②如图,过点C作CF∥BE,交AD的延长线于点F,在AD上取一点G,使得CG=CF,
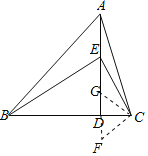
∵∠BAC=∠BED=2∠CED=α,
∴∠ABE=∠CAG,∠F=∠BED=α=∠CGF,
∴∠AEB=∠AGC,
∴△ABE∽△CAG,
∴![]() =
=![]() .
.
∵CF∥BE,
∴△BED∽△CFD,
∴![]() =
=![]() =3.
=3.
设CF=x,BE=3x,AE=y,则CG=EG=x,
∴![]() =
=![]() .
.
解得:![]() =
=![]() ,
,
∴![]() =
=![]() ;
;
(2)如图,过点C作CF∥AD,交BA的延长线于F,延长BE交CF与G,

则∠BAD=∠F,∠DAC=∠ACF,
又∵AD为△ABC的角平分线,即∠BAD=∠DAC,
∴∠ACF=∠F,
∴AF=AC=5,
又AE=ED,
∴FG=CG,
∴AG⊥CF,
∴∠CAG=∠FAG,
∴AD⊥AG,
∵tan∠BED=2,
∴tan∠AEG=2,
∵AE=ED=2,
∴![]() =2,
=2,
∴AG=2AE=4,
又∵AC=5,
∴FG=CG=3,
∵DE∥CG,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得BE=4![]() .
.