题目内容
【题目】如图,在△ABC中,∠C=120°,AB=4cm,两等圆⊙A与⊙B外切,则图中两个扇形(即阴影部分)的面之和为cm2 . (结果保留π).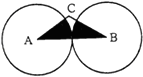
【答案】![]() π
π
【解析】解:∵两等圆⊙A与⊙B外切, 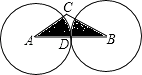
∴AD=BD= ![]() AB=2,
AB=2,
∵∠C=120°
∴∠CAB+∠CBA=60°
设∠CAB=x°,∠CBA=y°
则x+y=60
∴图中两个扇形(即阴影部分)的面积之和为 ![]() +
+ ![]() =
= ![]() =
= ![]() =
= ![]() π,
π,
所以答案是: ![]() π.
π.
【考点精析】关于本题考查的三角形的内角和外角和相切两圆的性质,需要了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;如果两圆相切,那么切点一定在连心线上,它们是轴对称图形,对称轴是两圆的连心线才能得出正确答案.

练习册系列答案
相关题目