题目内容
【题目】在平面直角坐标系中,点P在第一象限角平分线上,点A在x轴的正半轴运动,点B在y轴上,且![]() .
.
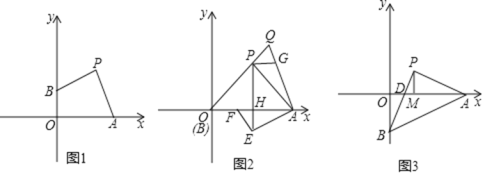
![]() 如图1,点B在y轴的正半轴上,
如图1,点B在y轴的正半轴上,![]() ,
,![]() ,则
,则![]() ______;
______;
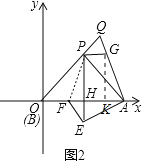
![]() 如图2,点B与原点重合,
如图2,点B与原点重合,![]() ,点Q是OP延长线上一点,连接QA,过点P作
,点Q是OP延长线上一点,连接QA,过点P作![]() 轴,与QA相交于点G,过点P作x轴的垂线,垂足是点H,过点A作QA的垂线与PH相交于点E,过点E作
轴,与QA相交于点G,过点P作x轴的垂线,垂足是点H,过点A作QA的垂线与PH相交于点E,过点E作![]() ,与x轴相交于点F,若
,与x轴相交于点F,若![]() ,求点E的坐标;
,求点E的坐标;
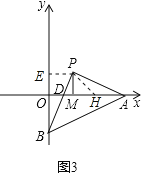
![]() 如图3,点B在y轴的负半轴上,PB与x轴相交于点D,连接AB,AO平分
如图3,点B在y轴的负半轴上,PB与x轴相交于点D,连接AB,AO平分![]() ,过点P作
,过点P作![]() 轴于点M,求
轴于点M,求![]() 的值.
的值.
【答案】(1)2;(2)![]() ;(3)2.
;(3)2.
【解析】
![]() 如图1中,作
如图1中,作![]() 轴于E,
轴于E,![]() 于
于![]() 只要证明四边形PEOF是正方形,
只要证明四边形PEOF是正方形,![]() ≌
≌![]() 即可解决问题;
即可解决问题;![]() 如图2中,连接PF,作
如图2中,连接PF,作![]() 于
于![]() 证明四边形PFAG是等腰梯形,可得四边形PGKH是矩形,
证明四边形PFAG是等腰梯形,可得四边形PGKH是矩形,![]() ≌
≌![]() ,推出
,推出![]() ,PG=HK,由
,PG=HK,由![]() ,推出
,推出![]() ,由此即可解决问题;
,由此即可解决问题;![]() 如图3中,作
如图3中,作![]() 轴于E,在MA上取一点H,使得
轴于E,在MA上取一点H,使得![]() ,连接
,连接![]() 首先证明
首先证明![]() 是等腰直角三角形,由OA平分
是等腰直角三角形,由OA平分![]() ,推出
,推出![]() ,
,![]() ,由
,由![]() ,推出∠PHM=45°=∠HAP+∠HPA
,推出∠PHM=45°=∠HAP+∠HPA
,推出![]() ,推出
,推出![]() ,设
,设![]() ,
,![]() ,则PH=AH=
,则PH=AH=![]() y,因为
y,因为![]() ,推出
,推出![]() ,可得
,可得![]() ,可得
,可得![]() .
.
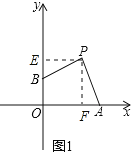
![]() 如图1中,作
如图1中,作![]() 轴于E,
轴于E,![]() 于F.
于F.
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形PEOF是矩形,
四边形PEOF是矩形,
![]() ,
,
![]() 四边形PEOF是正方形,
四边形PEOF是正方形,
![]() ,
,![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
故答案为2.
![]() 如图2中,连接PF,作
如图2中,连接PF,作![]() 于K.
于K.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形PFAG是等腰梯形,
四边形PFAG是等腰梯形,
易证四边形PGKH是矩形,![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]()
![]() 如图3中,作
如图3中,作![]() 轴于E,在MA上取一点H,使得
轴于E,在MA上取一点H,使得![]() ,连接PH.
,连接PH.
![]() ,
,
![]() ,
,
![]() 四边形PEOM是矩形,
四边形PEOM是矩形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,设
,设![]() ,
,![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目