题目内容
【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.
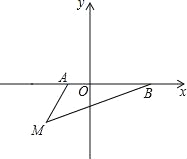
(1)填空:a= ,b= ;
(2)如果在第三象限内有一点M(﹣2,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=![]() 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
【答案】(1)a=-1,b=3;
(2)S△ABM=-2m
(3)P点坐标为(0, ![]() )或(7,0)或(0,
)或(7,0)或(0, ![]() )
)
【解析】试题分析:(1)根据非负数的意义,可直接求出求出a、b的值;
(2)作MC⊥AB于C,由M点在第三象限,可结合头像变化,然后再讨论,根据三角形的面积求解出三角形的面积即可;
(3)根据题意,可分为在x轴上或y轴上,然后根据割补法求三角形的面积,确定点的坐标.
试题解析:
解:(1)填空:a=-1 ,b= 3 ;
(2)作MC⊥AB于C,
由点M(﹣2,m)在第三象限,则MC=|m|=-m,
又A(-1,0),B(3,0),则AB=4,
S△ABM=0.5×AB×MC=0.5×4×(-m)=-2m
(3)由m=![]() ,则S△ABM=-2m=3,
,则S△ABM=-2m=3,
当P在x轴上时,S△pBM=S△ABM即![]() ,因此
,因此
BP=AB=4,因此点P的坐标为(7,0);
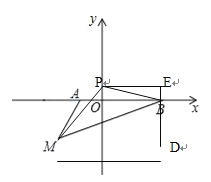
当P在y轴的正半轴时,如图,S△pBM=S△ABM=3,分别过点P、B、M作PE∥x轴,MD∥x轴,DE∥y轴,
令点P(0,n)则PE=3,BE=n,ED=n+![]() ,BD=
,BD=![]() ,MD=5,由S梯形MDEP= S△pBM + S△DBM + S△pBE
,MD=5,由S梯形MDEP= S△pBM + S△DBM + S△pBE
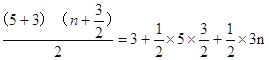
即,解得n=0.3,则P(0,![]() )
)
当P在y轴负半轴且在MB下方时,求得P(0.,![]() )
)

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目