Question

【题目】如图所示，点O是∠EPF平分线上的一点，以点O为圆心的圆与角的两边分别交于点A、B和C、D． 求证：AB=CD；

Answer 1

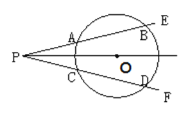
【答案】详见解析

【解析】

过点O分别作PB、PD的垂线，垂足分别为M、N，连接OA、OC，根据角平分线性质得出ON=OM，根据勾股定理求出AM=CN，根据垂径定理得出AB=2AM，CD=2CN，即可得出答案．

证明：过点O分别作PB、PD的垂线，垂足分别为M、N，连接OA、OC，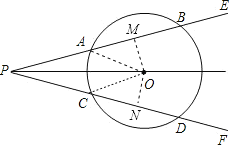

则∠OMA=∠ONC=90°，
∵点O是∠EPF的平分线上，
∴OM=ON，
在Rt△AMO和Rt△ONC中，由勾股定理得：AM2=OA2-OM2，CN2=OC2-ON2，
∵OC=OA，
∴AM=CN，
∵OM、ON过O，OM⊥AB，ON⊥CD，
∴AB=2AM，CD=2CN，
∴AB=CD．