题目内容
【题目】如图,在正方形![]() 中,点
中,点![]() 、
、![]() 是正方形内两点,
是正方形内两点,![]() ,
,![]() ,为探索这个图形的特殊性质,某数学兴趣小组经历了如下过程:
,为探索这个图形的特殊性质,某数学兴趣小组经历了如下过程:
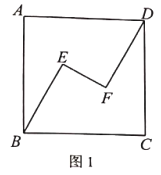
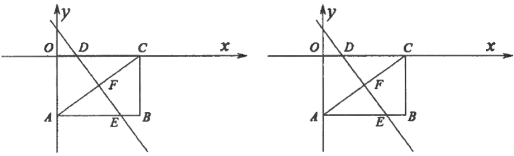
(1)在图1中,连接![]() ,且
,且![]()
①求证:![]() 与
与![]() 互相平分;
互相平分;
②求证:![]() ;
;
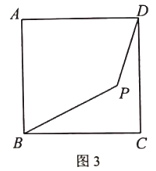
(2)在图2中,当![]() ,其它条件不变时,
,其它条件不变时,![]() 是否成立?若成立,请证明:若不成立,请说明理由.
是否成立?若成立,请证明:若不成立,请说明理由.
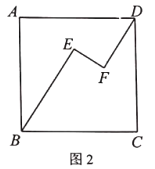
(3)在图3中,当![]() ,
,![]() ,
,![]() 时,求
时,求![]() 之长.
之长.
【答案】(1)①详见解析;②详见解析;(2)当BE≠DF时,(BE+DF)2+EF2=2AB2仍然成立,理由详见解析;(3)![]()
【解析】
(1)①连接ED、BF,证明四边形BEDF是平行四边形,根据平行四边形的性质证明;②根据正方形的性质、勾股定理证明;
(2)过D作DM⊥BE交BE的延长线于M,连接BD,证明四边形EFDM是矩形,得到EM=DF,DM=EF,∠BMD=90°,根据勾股定理计算;
(3)过P作PE⊥PD,过B作BELPE于E,根据(2)的结论求出PE,结合图形解答.
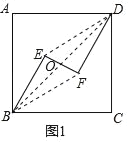
(1)证明:①连接ED、BF,
∵BE∥DF,BE=DF,
∴四边形BEDF是平行四边形,
∴BD、EF互相平分;
②设BD交EF于点O,则OB=OD=![]() BD,OE=OF=
BD,OE=OF=![]() EF.
EF.
∵EF⊥BE,
∴∠BEF=90°.
在Rt△BEO中,BE2+OE2=OB2.
∴(BE+DF)2+EF2=(2BE)2+(2OE)2=4(BE2+OE2)=4OB2=(2OB)2=BD2.
在正方形ABCD中,AB=AD,BD2=AB2+AD2=2AB2.
∴(BE+DF)2+EF2=2AB2;
(2)解:当BE≠DF时,(BE+DF)2+EF2=2AB2仍然成立,
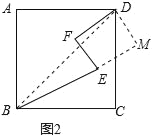
理由如下:如图2,过D作DM⊥BE交BE的延长线于M,连接BD.
∵BE∥DF,EF⊥BE,
∴EF⊥DF,
∴四边形EFDM是矩形,
∴EM=DF,DM=EF,∠BMD=90°,
在Rt△BDM中,BM2+DM2=BD2,
∴(BE+EM)2+DM2=BD2.
即(BE+DF)2+EF2=2AB2;
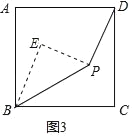
(3)解:过P作PE⊥PD,过B作BE⊥PE于E,
则由上述结论知,(BE+PD)2+PE2=2AB2.
∵∠DPB=135°,
∴∠BPE=45°,
∴∠PBE=45°,
∴BE=PE.
∴△PBE是等腰直角三角形,
∴BP=![]() BE,
BE,
∵![]() BP+2PD=4
BP+2PD=4![]() ,
,
∴2BE+2PD=4![]() ,即BE+PD=2
,即BE+PD=2![]() ,
,
∵AB=4,
∴(2![]() )2+PE2=2×42,
)2+PE2=2×42,
解得,PE=2![]() ,
,
∴BE=2![]() ,
,
∴PD=2![]() ﹣2
﹣2![]() .
.