题目内容
【题目】在长方形
中，
，
，现将长方形向右平移
，再向下平移
后到长方形
的位置.
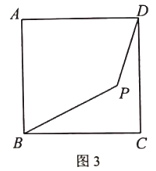
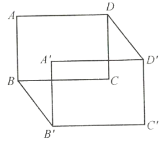
（1）如图，用
的代数式表示长方形与长方形的重叠部分的面积，这时应满足怎样的条件？
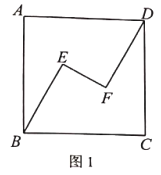
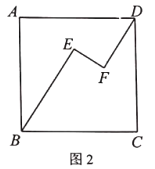
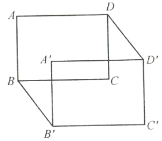
（2）如图，用的代数式表示六边形
的面积；
（3）当这两个长方形没有重叠部分时，第（2）小题的结论是否改变，请说明理由.
【答案】（1）
，
应满足的条件是：
；（2）
；（3）不改变，理由详见解析.
【解析】
（1）表示出重叠部分的长与宽，然后根据长方形的面积公式列式整理即可，根据重叠部分的宽为正数求x的取值范围；
（2）方法一：利用平移前后的长方形的面积的和加上两个正方形的面积，然后再减去重叠部分的面积列式进行计算即可得解；
方法二：利用六边形所在的长方形的面积减去两个小直角三角形的面积，根据面积公式列式进行计算即可得解．
（3）当这两个长方形没有重叠部分时，第（2）小题的结论不改变，延长AD、C′D′交于点M，延长AB、C′B′交于点N，利用S六边形ABB′C′D′D=S四边形ANC′M-2S△BNB′求出即可．
解：（1）∵AB=8cm，BC=10cm，
∴重叠部分的长为（10-x），宽为[8-（x+1）]，
∴重叠部分的面积
∵8-（x+1）＞0，
解得x＜7，
∴x应满足的条件是：0≤x＜7；
（2）方法一：S=10×8×2+
x（x+1）×2-（x2-17x+70），
=160+x2+x-x2+17x-70，
=18x+90（cm2）（0≤x＜7）；
方法二：S=（10+x）（8+x+1）-x（x+1）×2，
=（10+x）（9+x）-x2-x，
=90+19x+x2-x2-x，
=18x+90（cm2）（0≤x＜7）．
（3）当这两个长方形没有重叠部分时，第（2）小题的结论不改变．
延长AD、C′D′交于点M，延长AB、C′B′交于点N，
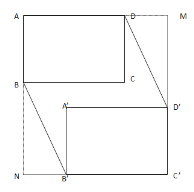
S六边形ABB′C′D′D=S四边形ANC′M-2S△BNB′=（10+x）（9+x）-2×x（x+1）=（18x+90）（cm2）．
∴当这两个长方形没有重叠部分时，第（2）小题的结论不改变.
【题目】新华文具用品店最近购进了一批钢笔，进价为每支6元，为了合理定价，在销售前4天试行机动价格，卖出时每支以10元为标准，超过10元的部分记为正，不足10元的部分记为负。文具店记录了这四天该钢笔的售价情况和售出情况，如下表所示：
第1天 | 第2天 | 第3天 | 第4天 | |
每支价格相对标准价格(元) | +1 | 0 | -1 | -2 |
售出支数(支) | 12 | 15 | 32 | 33 |
(1)填空：这四天中赚钱最多的是第______天，这天赚了______元钱；
(2)求新华文具用品店这四天出售这种钢笔一共赚了多少钱；
(3)新华文具用品店准备用这四天赚的钱全部购进这种钢笔，进价仍为每支6元为了促销这种钢笔，每只钢笔的售价在10元的基础上打九折，本次购进的这种钢笔全部售出后共赚了多少钱?
