题目内容
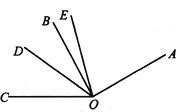
【题目】如图，OD是∠BOC的平分线，OE是∠AOC的平分线，∠AOB︰∠BOC=3︰2，若∠BOE=13°，求∠DOE的度数.
【答案】39°.
【解析】
设∠AOB=3x，∠BOC=2x．则∠AOC=∠AOB+∠BOC=5x．由角平分线定义和已知条件求出x=26°，即可得出所求角的度数．
解：设∠AOB=3x，∠BOC=2x．
则∠AOC=∠AOB+∠BOC=5x．
∵OE是∠AOC的平分线，
∴∠AOE═
∠AOC＝
x，
∴∠BOE=∠AOB-∠AOE=3xx＝x，
∵∠BOE=13°，
∴x＝13°，
解得：x=26°，
∵OD是∠BOC的平分线，
∴∠BOD＝∠BOC＝x＝26°，
∴∠DOE=∠DOB+∠BOE=26°+13°=39°．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
【题目】有20筐白菜，以每筐25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：
与标准质量的差值（单位：千克） |
|
|
| 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
（1）20筐白菜中，最重的一筐比最轻的一筐多重多少千克？
（2）与标准重量比较，20筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价2.8元，则出售这20筐白菜可卖多少元？（结果保留整数）