题目内容
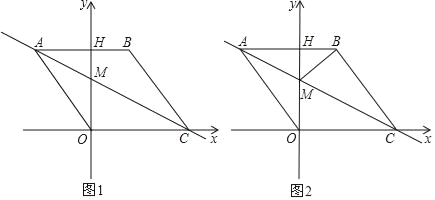
【题目】如图,矩形![]() 的两条边
的两条边![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,已知点
轴上,已知点![]() 坐标为(4,–3).把矩形
坐标为(4,–3).把矩形![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,直线
处,直线![]() 与
与![]() 、
、![]() 、
、![]() 的交点分别为
的交点分别为![]() 、
、![]() 、
、![]() .
.
(1)线段![]() ;
;
(2)求点![]() 坐标及折痕
坐标及折痕![]() 的长;
的长;
(3)若点![]() 在
在![]() 轴上,在平面内是否存在点
轴上,在平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,则请求出点
为顶点的四边形是菱形?若存在,则请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
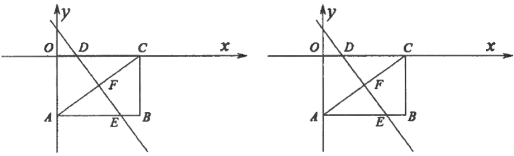
【答案】(1)![]() ;(2)
;(2)![]() ;拆痕DE的长为
;拆痕DE的长为![]() ; (3)点Q坐标为
; (3)点Q坐标为![]()
【解析】
(1)根据B点的坐标即可求得AC的长度.
(2)首先根据已知条件证明![]() ,再根据相似比例计算DF、CD的长度
,再根据相似比例计算DF、CD的长度
即可计算出D点的坐标,再证明![]() ,根据EF=DF,即可计算的DE的长度.
,根据EF=DF,即可计算的DE的长度.
(3)根据等腰三角形的性质,分类讨论第一种情况当![]() 时;第二种情况当
时;第二种情况当![]() 时;第三种情况当
时;第三种情况当![]() 时,分别计算即可.
时,分别计算即可.
解:(1)![]()
(2)![]() ,由折叠可得:
,由折叠可得:![]()
![]() ,
,![]()
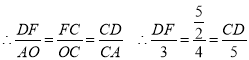 .
.
![]()
![]()
∵四边形OABC是矩形,
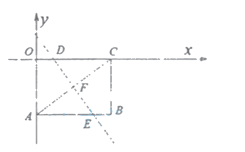
![]()
![]()
![]()
∴拆痕DE的长为![]()
(3)由(2)可知,![]() ,
,
![]()
若以P、D、E、Q为顶点的四边形是菱形,则![]() 必为等腰三角形。
必为等腰三角形。
当![]() 时,可知
时,可知![]() ,
,
此时PE为对角线,可得![]()
当![]() 时,可知
时,可知![]() ,此时DP为对角线,可得
,此时DP为对角线,可得![]() ;
;
当![]() 时,P与C重合,Q与A重合,
时,P与C重合,Q与A重合,![]()
综上所述,满足条件的点Q坐标为![]()

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克) |
|
|
| 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.8元,则出售这20筐白菜可卖多少元?(结果保留整数)