题目内容
【题目】△ABC中，∠A=40°，若点O是△ABC的外心，则∠BOC=_____°；若点I是△ABC的内心，则∠BIC=_____°．
【答案】80110．
【解析】
根据题意画出图形，根据圆周角定理求出即可，再根据题意，求出∠IBC+∠ICB度数，根据三角形内角和定理即可求出∠BIC．
如图1时，
由圆周角定理得：∠BOC=2∠A=2×40°=80°；
如图2时，
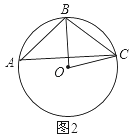
同样由圆周角定理得：∠BOC=2∠A=80°；
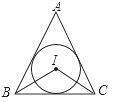
∵∠A+∠ABC+∠ACB=180°，∠A=40°，
∴∠ABC+∠ACB=140°，
∵I是△ABC的内心，
∴∠IBC=
∠ABC，∠ICB=∠ACB，
∴∠IBC+∠ICB=×140°=70°，
∴∠BIC=180°﹣（∠IBC+∠ICB）=110°，
故答案为：80，110．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
