ЬтФПФкШн
ЁОЬтФПЁПВЮеебЇЯАКЏЪ§ЕФЙ§ГЬгыЗНЗЈЃЌЬНОПКЏЪ§![]()
![]() ЕФЭМЯѓгыаджЪЃЎвђЮЊ
ЕФЭМЯѓгыаджЪЃЎвђЮЊ![]() ЃЌМД
ЃЌМД![]() ЃЌЫљвдЮвУЧЖдБШКЏЪ§
ЃЌЫљвдЮвУЧЖдБШКЏЪ§![]() РДЬНОПЃЎ
РДЬНОПЃЎ
СаБэЃК
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
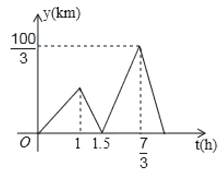
УшЕуЃКдкЦНУцжБНЧзјБъЯЕжаЃЌвдздБфСП![]() ЕФШЁжЕЮЊКсзјБъЃЌвд
ЕФШЁжЕЮЊКсзјБъЃЌвд![]() ЯргІЕФКЏЪ§жЕЮЊзнзјБъЃЌУшГіЯргІЕФЕуЃЌШчЭМЫљЪОЃК
ЯргІЕФКЏЪ§жЕЮЊзнзјБъЃЌУшГіЯргІЕФЕуЃЌШчЭМЫљЪОЃК
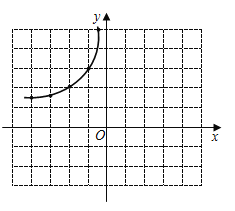
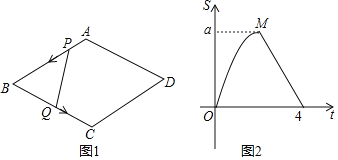
ЃЈ1ЃЉЧыВЙШЋКЏЪ§ЭМЯѓЃЛ
ЃЈ2ЃЉЙлВьЭМЯѓВЂЗжЮіБэИёЃЌЛиД№ЯТСаЮЪЬтЃК
ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖј_________ЃЛЃЈЬюЁАдіДѓЁБЛђЁАМѕаЁЁБЃЉ
ЕФдіДѓЖј_________ЃЛЃЈЬюЁАдіДѓЁБЛђЁАМѕаЁЁБЃЉ
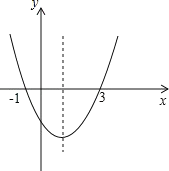
Ђк![]() ЕФЭМЯѓЪЧгЩ
ЕФЭМЯѓЪЧгЩ![]() ЕФЭМЯѓЯђ________ЦНвЦ________ИіЕЅЮЛЖјЕУЕНЃЛ
ЕФЭМЯѓЯђ________ЦНвЦ________ИіЕЅЮЛЖјЕУЕНЃЛ
ЂлЭМЯѓЙигкЕу_________жааФЖдГЦЃЎЃЈЬюЕуЕФзјБъЃЉ
ЃЈ3ЃЉНсКЯКЏЪ§ЭМЯѓЃЌЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћЯъНтЃЛЃЈ2ЃЉдіДѓЃЌЩЯЃЌ1ЃЌЃЈ0ЃЌ1ЃЉЃЛЃЈ3ЃЉЉ1ЃМxЃМ0ЛђxЃО1
ЁОНтЮіЁП
ЃЈ1ЃЉгУЙтЛЌЧњЯпЫГДЮСЌНгМДПЩЃЛ
ЃЈ2ЃЉРћгУЭМЯѓЗЈМДПЩНтОіЮЪЬтЃЛ
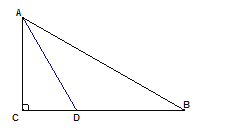
ЃЈ3ЃЉСЊСЂЗНГЬЧѓГіЕуAЁЂBЕФзјБъЃЌгЩДЫМДПЩНтОіЮЪЬтЃЎ
НтЃКЃЈ1ЃЉКЏЪ§ЭМЯѓШчЭМЫљЪОЃК
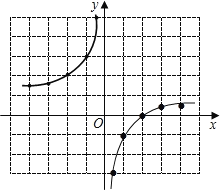
ЃЈ2ЃЉЂйЕБxЃМ0ЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЛ
Ђк![]() ЕФЭМЯѓЪЧгЩyЃН
ЕФЭМЯѓЪЧгЩyЃН![]() ЕФЭМЯѓЯђЩЯЦНвЦ1ИіЕЅЮЛЖјЕУЕНЃЛ
ЕФЭМЯѓЯђЩЯЦНвЦ1ИіЕЅЮЛЖјЕУЕНЃЛ
ЂлЭМЯѓЙигкЕуЃЈ0ЃЌ1ЃЉжааФЖдГЦЃЎ
ЙЪД№АИЮЊЃКдіДѓЃЌЩЯЃЌ1ЃЌЃЈ0ЃЌ1ЃЉЃЛ
ЃЈ3ЃЉИљОнЬтвтЕУЃК![]() ЃНЉ2x+1ЃЌНтЕУЃКxЃНЁР1ЃЌ
ЃНЉ2x+1ЃЌНтЕУЃКxЃНЁР1ЃЌ
ЕБxЃН1ЪБЃЌyЃНЉ2x+1ЃНЉ1ЃЌ
ЕБxЃНЉ1ЪБЃЌyЃНЉ2x+1ЃН3ЃЌ
ЁрНЛЕуЮЊЃЈ1ЃЌЉ1ЃЉЃЌЃЈЉ1ЃЌ3ЃЉЃЌ
ЁрЕБ![]() ЃОЉ2x+1ЪБЃЌЧѓxЕФШЁжЕЗЖЮЇЮЊЉ1ЃМxЃМ0ЛђxЃО1ЃЎ
ЃОЉ2x+1ЪБЃЌЧѓxЕФШЁжЕЗЖЮЇЮЊЉ1ЃМxЃМ0ЛђxЃО1ЃЎ

 ЦкФЉ100ЗжДГЙиКЃЕэПМЭѕЯЕСаД№АИ
ЦкФЉ100ЗжДГЙиКЃЕэПМЭѕЯЕСаД№АИ