题目内容
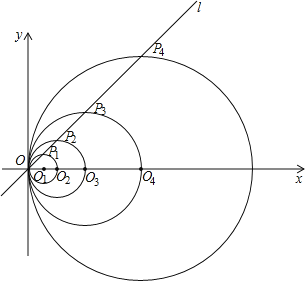
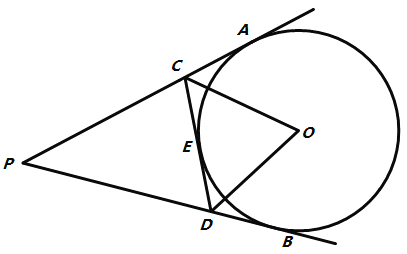
【题目】已知:如图,![]() 分别切
分别切![]() 于点
于点![]() 点.
点.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,求
,求![]() 的周长.
的周长.
【答案】(1)70°;(2)![]()
【解析】
(1)连接OA、OB和OE,根据圆的切线性质求出∠AOB的度数,再次利用圆的切线的性质求出∠AOC=∠EOC=![]() 和∠EOD=
和∠EOD=![]() ∠EOB,即可得出答案;
∠EOB,即可得出答案;
(2)根据切线长定理得出CE=CA,DE=DB,PA=PB,再结合周长公式计算即可得出答案.
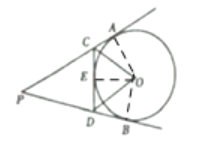
(1)连接OA、OB和OE
∵点A和点B均为圆O的切点
∴∠PAO=∠PBO =90°
∴∠AOB=360°-∠P-∠PAO-∠PBO=140°
又CA和CE均为圆的切线
∴∠ACO=∠ECO,∠OAC=∠OEC=90°
∴∠AOC=∠EOC=![]()
同理可得∠EOD=![]() ∠EOB
∠EOB
∴∠COD=∠EOC+∠EOD=![]() =70°
=70°
(2)∵PA、PB和CD分别切圆O于点A、B和E点
∴CE=CA,DE=DB,PA=PB
∴△PCD的周长=PC+PD+CD=PC+AC+PD+DB=PA+PB=2PA=20cm

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目