题目内容
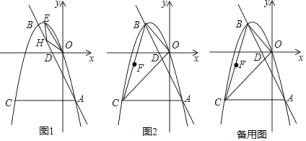
【题目】已知抛物线![]() 经过点
经过点![]() .设点
.设点![]() ,请在抛物线的对称轴上确定一点
,请在抛物线的对称轴上确定一点![]() ,使得
,使得![]() 的值最大,则
的值最大,则![]() 点的坐标为________.
点的坐标为________.
【答案】![]()
【解析】
首先利用待定系数法求得抛物线的解析式,然后可求得抛物线的对称轴方程x=2,又由作点C关于x=2的对称点C′,直线AC′与x=2的交点即为D,求得直线AC′的解析式,即可求得答案.
∵抛物线![]() 经过点A(4,0),
经过点A(4,0),
∴![]() ,
,
∴b=2,
∴抛物线的解析式为:![]()
∴抛物线的对称轴为:直线x=2,
∵点C(1,3),
∴作点C关于x=2的对称点C′(3,3),
直线AC′与x=2的交点即为D,
因为任意取一点D(AC与对称轴的交点除外)都可以构成一个△ADC.而在三角形中,两边之差小于第三边,即|ADCD|<AC′.所以最大值就是在D是AC′延长线上的点的时候取到|ADC′D|=AC′.把A,C′两点坐标代入,得到过AC′的直线的解析式即可;
设直线AC′的解析式为y=kx+b,
∴![]()
解得:![]()
∴直线AC′的解析式为y=3x12,
当x=2时,y=6,
∴D点的坐标为(2,6).

故答案为:(2,6).

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目