题目内容
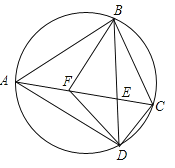
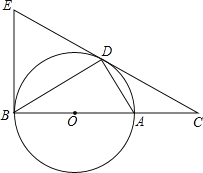
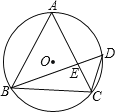
【题目】如图,已知△ABC内接于⊙O,D是⊙O上一点,连接BD、CD、AC、BD交于点E.
(1)请找出图中的相似三角形,并加以证明;
(2)若∠D=45°,BC=2,求⊙O的面积.
【答案】(1)△ABE∽△DCE,证明详见解析;(2)2π.
【解析】
(1)容易发现:△ABE与△DCE中,有两个角对应相等,根据相似三角形的判定可得到它们相似;
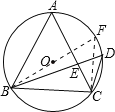
(2)求⊙O的面积,关键是求⊙O的半径,为此作⊙O的直径BF,连接CF,得出△BCF是等腰直角三角形,由BC=2,求出BF的长,从而求出⊙O的面积.
解:(1)结论:△ABE∽△DCE,
证明:在△ABE和△DCE中,
∵∠A=∠D,∠AEB=∠DEC,
∴△ABE∽△DCE.
(2)作⊙O的直径BF,连接CF,
∴∠F=∠D=45°,∠BCF=90°.
∴△BCF是等腰直角三角形.
∵FC=BC=2,
∴BF=2![]() .
.
∴OB=![]() .
.
∴S⊙O=OB2π=2π.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目