题目内容
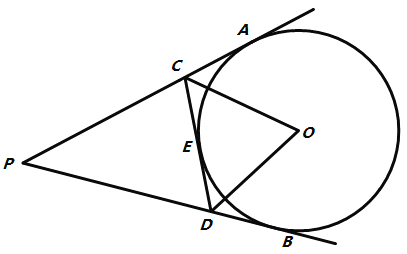
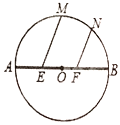
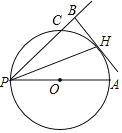
【题目】如图,在⊙O中,PA是直径,PC是弦,PH平分∠APB且与⊙O交于点H,过H作HB⊥PC交PC的延长线于点B.
(1)求证:HB是⊙O的切线;
(2)若HB=4,BC=2,求⊙O的直径.
【答案】(1)详见解析;(2)10.
【解析】
(1)连接OH,由题意可得∠OHP=∠HPA=∠HPB,可证OH∥BP,则可得OH⊥BH,根据切线的判定可证HB是⊙O的切线;
(2)过点O作OE⊥PC,垂足为E,可证四边形EOHB是矩形,可得OE=BH=4,OH=BE,再根据勾股定理可求OP的长,即可得⊙O的直径.
证明:(1)如图,连接OH,
∵PH平分∠APB,
∴∠HPA=∠HPB,
∵OP=OH,
∴∠OHP=∠HPA,
∴∠HPB=∠OHP,
∴OH∥BP,
∵BP⊥BH,
∴OH⊥BH,
∴HB是⊙O的切线;
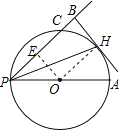
(2)如图,过点O作OE⊥PC,垂足为E,
∵OE⊥PC,OH⊥BH,BP⊥BH,
∴四边形EOHB是矩形,
∴OE=BH=4,OH=BE,
∴CE=OH﹣2,
∵OE⊥PC
∴PE=EC=OH﹣2=OP﹣2,
在Rt△POE中,OP2=PE2+OE2,
∴OP2=(OP﹣2)2+16
∴OP=5,
∴AP=2OP=10,
∴⊙O的直径是10.

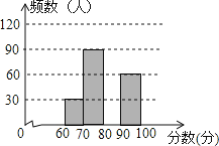
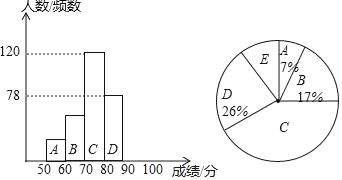
【题目】 为了解今年师大附中多元校区共3000名八年级学生“地理知识大赛”的笔试情况,随机抽取了部分参赛同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据表中提供的信息,解答下列问题:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.1 |
70≤x<80 | 90 | n |
80≤x<90 | m | 0.4 |
90≤x≤100 | 60 | 0.2 |
(1)此次调查的样本容量为______;m=______;n=______;
(2)补全频数分布直方图;
(3)如果比赛成绩80分以上为优秀,那么你估计师大附中多元校区八年级学生笔试成绩的优秀人数大约是______名.