��Ŀ����
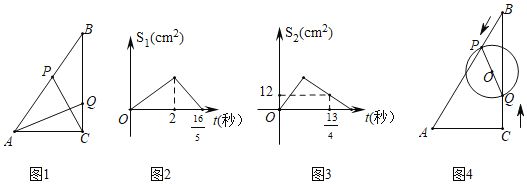
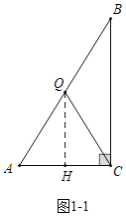
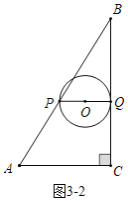
����Ŀ����ͼ��1������Rt��ABC�У���ACB��90�㣬AC��6cm������P�ӵ�B������������B��A��C·�������˶���Cֹͣ������Q�ӵ�C������������C��B��A·�������˶���Aֹͣ�����P��Qͬʱ�����˶�t�����ͼ��2���ǡ�BPC�����S1��cm2����t���룩�ĺ�����ϵͼ��ͼ��3���ǡ�AQC�����S2��cm2����t���룩�ĺ�����ϵͼ��
��1����P�˶��ٶ�Ϊ�� ��cm/�룻Q�˶����ٶ��� ��cm/�룻
��2������PQ����tΪ��ֵʱ��PQ��BC��
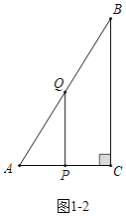
��3����ͼ��4�����˶�t��0��t��2����ʱ���Ƿ����������ʱ�̣�ʹ��PQΪֱ������O��Rt��ABC��һ�������У������ڣ����t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��5��4����2��t��![]() ����3�����ڣ�t��ֵΪ
����3�����ڣ�t��ֵΪ![]() ��1��
��1��![]() ��0��
��0��
��������
��1������·�̣��ٶȣ�ʱ��֮��Ĺ�ϵ�����֪����������⼴�ɣ�
��2����ͼ1��2�У���PQ��ACʱ������![]() ���ɴ˹������̼��ɽ�����⣻
���ɴ˹������̼��ɽ�����⣻
��3��������������ͼ3��1�У�����O��AB����ʱ��QP��AB������ͼ3��2�У�����O��BC����ʱ��QP��BC������ͼ3��3�У�����O��AC����ʱ�����е�ΪH������OH����PM��AC��M��PK��BC��K���ֱ�������⼴�ɣ�
�⣺��1����ͼ2��֪����![]() ��
��![]() �˶���
�˶���![]() ��ʱ��
��ʱ��![]() �룬
�룬
![]() ��
��![]() ���˶��ٶ�
���˶��ٶ�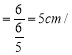 �룮
�룮
![]() ��
��
![]() ��
��
![]() ��
��
��ͼ![]() �У���
����![]() ��
��![]() ��
��
��ͼ3��֪��![]() ʱ��
ʱ��![]() �����Ϊ12��
�����Ϊ12��
![]()
![]() ��
��
![]()
![]() ��
��
![]() ��
��
![]() ��
��
![]()
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ���˶��ٶ�
���˶��ٶ�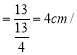 �룮
�룮
�ʴ�Ϊ5��4��
��2����ͼ![]() �У���
�У���![]() ʱ������
ʱ������![]() ��
��
![]()
![]() ��
��
���![]() ��
��
![]() ��
��![]() ��ʱ��
��ʱ��![]() ��
��
��3������ͼ![]() �У���
����![]() ��
��![]() ����ʱ��
����ʱ��![]() ��
��
![]() ��
��
![]()
![]() ��
��
![]()
![]() ��
��
![]()
����ͼ![]() �У���
����![]() ��
��![]() ����ʱ��
����ʱ��![]() ��
��
![]() ��
��
![]()
![]() ��
��
![]()
![]() ��
��
![]() ��
��
����ͼ![]() �У���
����![]() ��
��![]() ����ʱ�����е�Ϊ
����ʱ�����е�Ϊ![]() ������
������![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
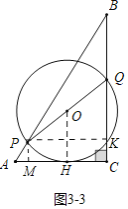
��![]() ��
��![]() ��
��
������![]() ��
��![]() ��
��
![]() �ı���
�ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��![]() ������
������![]() ��
��
���![]() ��0��
��0��
��������������������![]() ��ֵΪ
��ֵΪ![]() ��1��
��1��![]() ��0��
��0��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�