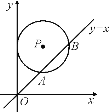
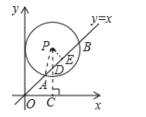
[题目]如图.在平面直角坐标系中.⊙P的圆心是.半径为2.函数y＝x的图象被⊙P截得的弦AB的长为2.则a的值是( )A. 2B. 2+2C. 2D. 2+ 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在平面直角坐标系中，⊙P的圆心是(2，a)(a＞2)，半径为2，函数y＝x的图象被⊙P截得的弦AB的长为2，则a的值是（）

A. 2B. 2＋2C. 2D. 2＋

【答案】D

【解析】

作辅助线,根据垂径定理得AE=,勾股定理得PE=1,证明△PDE为等腰直角三角形即可解题.

解：如图所示,过点P作PE⊥AB于E,点P作PC⊥x轴于C,交AB于D,连接PA.

∵AB=2,

∴AE=

又PA=2,

根据勾股定理得PE=1.

∵点D直线y=x上,故∠DOC=45°,

又∠DCO=90°,

∴∠ODC=45°,

∴∠PDE=∠ODC=45°,故∠DPE=∠PDE=45°,

∴DE= PE=1, PD=

又∵OC=2,

∴DC=OC=2,

故a=PD+DC=2+.

故选D

练习册系列答案

请根据统计图中的信息解答以下问题：

（1）本次抽取的学生人数是　　，扇形统计图中A所对应扇形圆心角的度数是　　．

（2）把条形统计图补充完整．

（3）若该学校共有2800人，等级达到优秀的人数大约有多少？

（4）A等级的4名学生中有3名女生1名男生，现在需要从这4人中随机抽取2人参加电视台举办的“中学生书法比赛”，请用列表或画树状图的方法，求被抽取的2人恰好是1名男生1名女生的概率．

【题目】如图，已知等边△ABC中边AB=10，按要求解答：

（1）尺规作图：作∠PBA，使得∠PBA=30°，射线BP交边AC于点P，（不写作法，保留作图痕迹）．

（2）在上图中，若点D在射线BP上，且使得AD=5，求BD的长（结果保留根号）．

【题目】已知：如图，分别切于点点．

（1）若，求；

（2）若，求的周长．

【题目】周老师为了了解学生自主学习、合作交流的具体情况，对本班部分学生进行了为期半年的跟踪调查，并将调查结果分成四类A：优；B：良；C：中；D：差．依据调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：

（1）本次调查中，周老师一共调查了______名学生；

（2）将统计图补充完整；

（3）为了共同进步，周老师想从被调查的A类和D类学生中分别选取一位同学进行“一对一”帮扶，请用列表法或画树形图的方法求所选的两位同学恰好是两位女同学的概率．

【题目】如图所示，点P位于等边△ABC的内部，且∠ACP=∠CBP．

(1)延长BP至点D，使得PD=PC，连接AD，CD．

①依题意，补全图形；

②证明：AD+CD=BD；

(2)在(1)的条件下，若BD的长为2，求四边形ABCD的面积．

【题目】如图，已知的直径，、为的三等分点，、为上两点，且，求的值.

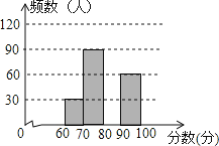
【题目】为了解今年师大附中多元校区共3000名八年级学生“地理知识大赛”的笔试情况，随机抽取了部分参赛同学的成绩，整理并制作如图所示的图表(部分未完成)．请你根据表中提供的信息，解答下列问题：

分数段	频数	频率
60≤x＜70	30	0.1
70≤x＜80	90	n
80≤x＜90	m	0.4
90≤x≤100	60	0.2

（1）此次调查的样本容量为______；m=______；n=______；

（2）补全频数分布直方图；

（3）如果比赛成绩80分以上为优秀，那么你估计师大附中多元校区八年级学生笔试成绩的优秀人数大约是______名．

【题目】如图，线段 AB 经过⊙O 的圆心， AC ， BD 分别与⊙O 相切于点 C ，D ．若 AC =BD = 4 ，∠A=45°，则弧CD的长度为（）

A.πB.2πC.2πD.4π

试题分类