题目内容
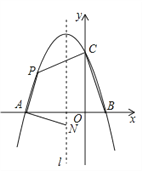
【题目】如图,把一块三角板放在直角坐标系第一象限内,其中30°角的顶点A落在y轴上,直角顶点C落在x轴的(![]() ,0)处,∠ACO=60°,点D为AB边上中点,将△ABC沿x轴向右平移,当点A落在直线y=x﹣3上时,线段CD扫过的面积为_____.
,0)处,∠ACO=60°,点D为AB边上中点,将△ABC沿x轴向右平移,当点A落在直线y=x﹣3上时,线段CD扫过的面积为_____.

【答案】12
【解析】
根据函数解析式和直角三角形的性质求出点D平移的距离和CD的长度,然后证明∠DCO=90°,再根据矩形的面积公式计算即可.
解:∵点C的坐标为(![]() ,0),∠ACO=60°,
,0),∠ACO=60°,
∴AC=![]() ,OA=3,
,OA=3,
∴点A的坐标为(0,3),
在y=x﹣3中,当y=3时,即3=x3,解得x=6,
∴当点A落在直线y=x3上时,点A平移的距离为6,此时点D平移的距离也是6,
∵∠ACO=60°,点D为AB边上中点,∠ACB=90°,∠CAD=30°,
∴DA=DC,
∴∠DCA=∠DAC=30°,
∴∠DCO=90°,
∵AC=![]() ,∠ACB=90°,∠CAB=30°,
,∠ACB=90°,∠CAB=30°,
∴BC2+AC2=AB2,即![]() ,
,
∴AB=4,
∴CD=2,
∴线段CD扫过的面积为:2×6=12,
故答案为:12.

练习册系列答案
相关题目