��Ŀ����
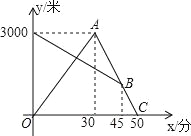
����Ŀ����֪�ı���ABCD�������Σ���P��ֱ��BC�ϣ���G��ֱ��AD�ϣ�P��G���������ζ����غϣ�����CD��ͬ�ࣩ��PD=PG��DF��PG�ڵ�H����ֱ��AB�ڵ�F�����߶�PG�Ƶ�P��ʱ����ת90���õ��߶�PE������EF��
��1����ͼ1������P���G�ֱ����߶�BC���߶�AD��ʱ��
����ֱ��д���߶�DG��PC��������ϵ(��Ҫ��֤������
����֤���ı���PEFD�����Σ�
��2����ͼ2������P���G�ֱ����߶�BC���߶�AD���ӳ�����ʱ��������ı���PEFD�������������ı��Σ���֤����IJ��룮


���𰸡���1����DG��2PC�����ɼ�������������������2���ı���PEFD�����Σ����ɼ�������
��������
��1�������ۣ�DG��2PC����ͼ1�У���PM��AD��M��ֻҪ֤���ı���PMDC�Ǿ��Σ��Ƴ�PC��DM����֤��MG��MD���ɽ�����⣮
�����ı���PMDC�Ǿ��ε�CD��PM���ɡ�ADF�ա�MPG���Ƴ�PG��PF�������ɵ�DP��PF����֤��DF��PE���Ƴ��ı���PEFD��ƽ���ı��Σ��ٽ��PD��PE����֤���ı���PEFD�����Σ�
��2����ͼ2�У���PM��AD��M�����ı���CDMP�Ǿ��Σ�CD��PM���ɡ�ADF�ա�MPG���Ƴ�DP��PG��PE��PF����֤��DF��PE���Ƴ��ı���PEFD��ƽ���ı��Σ���PD��PE������֤���ı���PEFD�����Σ�
�⣺��1�������ۣ�DG��2PC��
���ɣ���ͼ1�У���PM��AD��M��

���ı���ABCD�������Σ�
���C����CDM����DMP��90�㣬AD��CD��
���ı���DCPM�Ǿ��Σ�
��PC��DM��
��PD��PG��PM��DG��
��MG��MD��
��DG��2PC��
�߶�DG��PC��������ϵΪDG��2PC��
�ڡ��ı���CDMP�Ǿ��Σ�
��CD��PM��
��AD��CD��
��AD��PM��
��DF��PG��
���DAF����PMG����GHD��90�㣬
���ADF+��AFD��90�㣬��ADF +��PGM��90�㣬
���AFD����PGM��
�ڡ�ADF�͡�MPG�У�
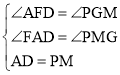 ��
��
���ADF�ա�GMP��
��DF��PG
��PG��PE��PD��
��DP��PG��PE��PD��
�ߡ�FHG����EPG��90�㣬
��DF��PE��
���ı���PEFD��ƽ���ı��Σ�
��PD��PE��
���ı���PEFD�����Σ�
��2�����ۣ��ı���PEFD�����Σ�
���ɣ���ͼ2�У���PM��AD��M�����ı���CDMP�Ǿ��Σ�CD��PM��
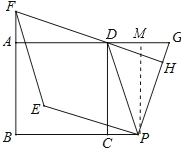
�ߡ�DAF����PMG����DHG��90�㣬
���ADF+��AFD��90�㣬��G+��GDH��90�㣬
�ߡ�ADF����GDH��
���AFD����G��
��AD��CD��CD��PM��
��AD��PM��
�ڡ�ADF�͡�MPG�У�
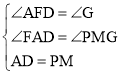 ��
��
���ADF�ա�MPG��
��DP��PG��PE��PD��
�ߡ�FHG����EPG��90�㣬
��DF��PE��
���ı���PEFD��ƽ���ı��Σ�
��PD��PE��
���ı���PEFD�����Σ�