题目内容
【题目】△ABC是等边三角形,点E、F分别为射线AC、射线CB上两点,CE=BF,直线EB、AF交于点D.
(1)当E、F在边AC、BC上时如图,求证:△ABF≌△BCE.

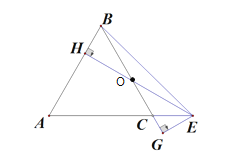
(2)当E在AC延长线上时,如图,AC=10,S△ABC=25![]() ,EG⊥BC于G,EH⊥AB于H,HE=8
,EG⊥BC于G,EH⊥AB于H,HE=8![]() ,EG= .
,EG= .

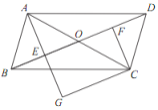
(3)E、F分别在AC、CB延长线上时,如图,BE上有一点P,CP=BD,∠CPB是锐角,求证:BP=AD.

【答案】(1)见解析;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)△ABC是等边三角形,由AB=BC,∠ABF=∠BCE=60°,证明全等即可;
(2)记BG,HE交于点O,先求出∠CEO=30°,即可求出AE的长,从而求出EG;
(3)先证明△ABF≌△BCE,再由BD=CP,∠CPB为锐角,证明△ABD≌△BCP即可.
(1)∵△ABC是等边三角形,
∴AB=BC,∠ABF=∠BCE=60°,
在△ABF和△ADF中
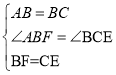
∴△ABF≌△BCE(SAS);
(2)记BG,HE交于点O,
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵EH⊥AB,EG⊥BG,
∴∠BHE=∠EGC=90°,
∴∠EOG=∠BOH=30°,
∴∠CEO=30°,∠CEG=30°,
∵HE=8![]() ,
,
∴AH=8,
∴AE=2AH=16,
∵AC=10,
∴CE=6,
∴CG=3,
∴EG=![]() ;
;
(3)∵△ABC为等边三角形,
∴AB=BC,∠ABC=∠ACB=60°,
∴∠ABF=∠BCE=120°,
在△ABF和△BCE中

∴△ABF≌△BCE(SAS),
∴AF=BE,∠AFB=∠BEC,∠FAB=∠EBC,
∵∠FBD=∠CBE,
∴∠FDB=∠BCE=120°,
∴∠ADB=60°,
∵△ABF≌△BCE(SAS),BD=CP,∠CPB为锐角,
∴∠CPB=∠BDA=60°,
在△ABD和△BCP中
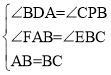
∴△ABD≌△BCP(AAS),
∴BP=AD.