Question

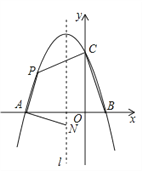
【题目】如图，抛物线 与x轴交于点A和点B（1，0），与y轴交于点C（0，3），其对称轴为=–1，P为抛物线上第二象限的一个动点．

（1）求抛物线的解析式并写出其顶点坐标；

（2）当点P的纵坐标为2时，求点P的横坐标；

（3）当点P在运动过程中，求四边形PABC面积最大时的值及此时点P的坐标．

Answer 1

【答案】（1）二次函数的解析式为，顶点坐标为（–1，4）；（2）点P横坐标为––1；（3）当时，四边形PABC的面积有最大值，点P（）．

【解析】试题分析: （1）已知抛物线 与轴交于点A和点B（1，0），与y轴交于点C（0，3），其对称轴为=﹣1，由此列出方程组，解方程组求得a、b、c的值，即可得抛物线的解析式，把解析式化为顶点式，直接写出顶点坐标即可；（2）把y=2代入解析式，解方程求得x的值，即可得点P的横坐标，从而求得点P的坐标；（3）设点Ｐ（，），则 ,根据得出四边形PABC与x之间的函数关系式，利用二次函数的性质求得x的值，即可求得点P的坐标.

试题解析:

（1）∵抛物线 与轴交于点A和点B（1，0），与y轴交于点C（0，3），其对称轴为=﹣1，

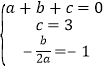∴　，　解得：，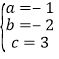

∴二次函数的解析式为 =，

∴顶点坐标为（﹣1，4）

（2）设点P（，2），

即=2，

解得=﹣1（舍去）或=﹣﹣1，

∴点P（﹣﹣1，2）.

（3）设点Ｐ（，），则 ,

,

∴ ＝

∴当时，四边形PABC的面积有最大值.

所以点P（）.