题目内容
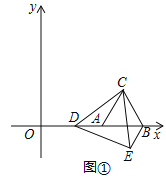
【题目】如图,在平面直角坐标系中,直线AB:y=kx+4(k≠0)与x轴,y轴,交于A、B两点,点C是BO的中点且tan∠ABO=![]()
(1)求直线AC的解析式;
(2)若点M是直线AC的一点,当![]() 时,求点M的坐标.
时,求点M的坐标.

【答案】(1)y=x+2(2)M(-6,-4),(2,4)
【解析】分析:(1)在Rt△ABO中求出OA的长,由点A,C的坐标即可求AC的解析式;(2)设M(m,m+2),则S△ABM=![]() ×|m-(-2)|BC,S△AOC=2,列方程求m.
×|m-(-2)|BC,S△AOC=2,列方程求m.
详解:(1)根据题意得,OB=4,又tan∠ABO=![]() ,
,
所以OA=2,则A(-2,0).
因为点C是BO的中点,所以OC=2,则C(0,2).
所以直线AC的解析式为y=x+2.
(2)设M(m,m+2),
因为S△AOC=2,S△ABM=![]() ×|m-(-2)|BC,
×|m-(-2)|BC,
所以![]() ×2|m-(-2)|=2×2,解得m=-6或m=2,
×2|m-(-2)|=2×2,解得m=-6或m=2,
当m=-6时,m+2=-4;
当m=2时,m+2=4.
所以M的坐标为(-6,-4),(2,4).

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目