题目内容
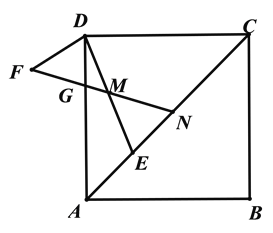
【题目】在菱形ABCD中,AC是对角线,CD=CE,连接DE,点M是线段DE的中点.
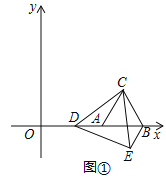
(1)如图1,连接CM,若AC=16,CD=10,求DE的长
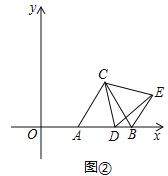
(2)如图2,点F在菱形的外部,DF=DM,且∠CDA=∠FDE,连接FM交AD于点G,FM的延长线交AC于点N,求证:CN=AG.
【答案】(1)2![]() (2)证明见解析
(2)证明见解析
【解析】分析:(1)过D作DP⊥AC交AC于P,由菱形的性质,勾股定理求得DP,EP的长;(2)连接AF,CM,分别用SAS证明△AFD≌△CME,ASA证明△AFG≌△MNC.
详解:(1)如图,
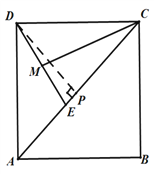
过D作DP⊥AC交AC于P,
∵DC=AD,DP⊥AC,∴CP=![]() AC=8.
AC=8.
又∵DC=10,∴DP=6.
∵EC=DC=10,∴AE=6.
∴EP=2,DE=![]() .
.
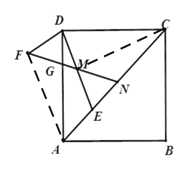
(2)连接AF,CM.
∵CD=CE,∴∠CDE=∠CED.
又∵∠CDA=∠FDE,∴∠FDA=∠CDE=∠CED.
在△AFD和△CME中
 ,
,
∴△AFD≌△CME.
∴∠FAD=∠MCE,AF=CM.
又∵FD=DM,∴∠DFM=∠DMF=∠EMN.
∵∠AFD=∠EMC,∠AFG+∠DFM=∠CMN+∠EMN
∴∠AFG=∠CMN
∴在△AFG和△MNC中
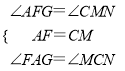 ,
,
∴△AFG≌△MNC,∴CN=AG.

 灵星计算小达人系列答案
灵星计算小达人系列答案【题目】西安市某中学九年级组织了一次数学计算比赛(禁用计算器),每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中A等级得分为100分,B等级得分为85分,C等级得分为75分,D等级得分为60分,数学教研组将九年级一班和二班的成绩整理并绘制成如下的统计图,请根据提供的信息解答下列问题.
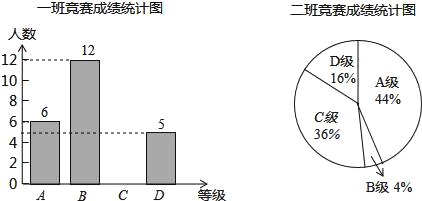
(1)把一班竞赛成绩统计图补充完整.
(2)填表:
平均数(分) | 中位数(分) | 众数(分) | |
一班 |
|
| 85 |
二班 | 84 | 75 |
|
(3)请从以下给出的两个方面对这次比赛成绩的结果进行①从平均数、众数方面来比较一班和二班的成绩;②从B级以上(包括B级)的人数方面来比较一班和二班的成绩.