题目内容
【题目】在平面直角坐标系xOy中,直线a:y=2x﹣6,和直线b:y=﹣ ![]() x+4相交于点H,分别与x、y轴交于点A、B、C、D,点P在x轴上,过点P作x轴的垂线,分别与直线a、b交于点E、F.
x+4相交于点H,分别与x、y轴交于点A、B、C、D,点P在x轴上,过点P作x轴的垂线,分别与直线a、b交于点E、F.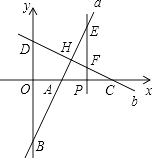
(1)求点H的坐标;
(2)判断直线a、b的位置关系,并说明理由;
(3)设点P的横坐标为m,当m为何值时,以D、E、F、O为顶点的四边形是
平行四边形,说明理由.
【答案】
(1)解:联立两直线解析式可得 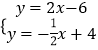 ,解得
,解得 ![]() ,
,
∴H(4,2);
(2)解:a⊥b,理由如下:
在y=2x﹣6中,令x=0,可得y=﹣6,在y=﹣ ![]() x+4中,令x=0可得y=4,
x+4中,令x=0可得y=4,
∴B(0,﹣6),D(0,4),
∴BD=10,DH= ![]() =2
=2 ![]() ,BH=
,BH= ![]() =4
=4 ![]() ,
,
∴DH2+DH2=20+80=100=BD2,
∴△BDH是以BD为斜边的直角三角形,
∴∠BHD=90°,即a⊥b;
(3)解:∵P点横坐标为m,
∴E(m,2m﹣6),F(m,﹣ ![]() m+4),
m+4),
∴EF=|2m﹣6﹣(﹣ ![]() m+4)|,
m+4)|,
当以D、E、F、O为顶点的四边形是平行四边形时,则EF=OD=4,
∴|2m﹣6﹣(﹣ ![]() m+4)|=4,解得m=
m+4)|=4,解得m= ![]() 或m=
或m= ![]() ,
,
∴当m的值为 ![]() 或
或 ![]() 时,以D、E、F、O为顶点的四边形是平行四边形.
时,以D、E、F、O为顶点的四边形是平行四边形.
【解析】(1)由两直线相交于点H,联立两直线解析式,求出方程组的解,得到点H的坐标;(2)根据题意求出B、D的坐标,根据两点间的距离公式求出DH、BH、BD的值,根据勾股定理的逆定理得到直角三角形,判断出直线a、b的位置是a⊥b;(3)根据P点横坐标为m,得到E、F点的坐标,求出EF的值,根据平行四边形的判定方法,得到m的值.

【题目】研究发现,地表以下岩层的温度与它所处的深度有表中所示的关系:
岩层的深度 | 1 | 2 | 3 | 4 | 5 | 6 | … |
岩层的温度 | 55 | 90 | 125 | 160 | 195 | 230 | … |
根据以上信息,回答下列问题:
(1)上表反映的两个变量之中,________是自变量,_______是因变量;
(2)岩层的深度![]() 每增加
每增加![]() ,温度
,温度![]() 是怎样变化的?试写出
是怎样变化的?试写出![]() 和
和![]() 的关系式;
的关系式;
(3)估计岩层![]() 深处的温度是多少?
深处的温度是多少?