Question

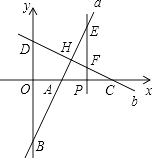
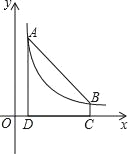
【题目】如图，点A（m，6），B（n，1）在反比例函数图象上，AD⊥x轴于点D，BC⊥x轴于点C，DC=5．

（1）求m，n的值并写出反比例函数的表达式；

（2）连结AB，在线段DC上是否存在一点E，使△ABE的面积等于5？若存在，求出点E的坐标；若不存在，请说明理由．

Answer 1

【答案】（1） （2）（5，0）

【解析】

（1）由反比例函数定义可知6m=n，m+5=n，联立可求解m和n的值，设反比例函数表达式为，代入A点坐标即可求解表达式；

（2）设E（x，0），则DE=x﹣1，CE=6﹣x，则可分别计算或表示出S四边形ABCD、S△ADE、S△BCE的面积，再由S△ABE=S四边形ABCD﹣S△ADE﹣S△BCE=5即可求解x的值.

（1）由题意得：，解得：，

∴A（1，6），B（6，1），

设反比例函数表达式为，

将A（1，6）代入得：k=6，

则反比例表达式为y=；

（2）存在，

设E（x，0），则DE=x﹣1，CE=6﹣x，

∵AD⊥x轴，BC⊥x轴，

∴∠ADE=∠BCE=90°，

连结AE，BE，

则S△ABE=S四边形ABCD﹣S△ADE﹣S△BCE

=（BC+AD）DC﹣DEAD﹣CEBC

=×（1+6）×5﹣（x﹣1）×6﹣（6﹣x）×1

=﹣x=5，

解得：x=5，

则E（5，0）．